EXERCISE-5A
Q1. What do you understand by the term up thrust of a fluid? Describe an experiment to show its existence.
Solution:
A b ody experiences an upward pull when it is partially or fully submerged in a liquid. An upthrust is the term for this upward thrust.
The experiment below can be used to show upthrust:
Use an airtight stopper to seal the mouth of an empty can. Put it in a bathtub that is full of water. It floats with the majority of its surface above the water’s surface and the remainder barely below. In the water, fling the can. You sense an upward thrust, making it challenging to lower the can farther into the water. It is observed that when the can is pushed further and deeper into the water, increasing amounts of force are required until the can is fully submerged. A significant force is still required to maintain the can’s resting posture when it is completely submerged in water. Again, it is seen that when the can is released in this position, it bounces back to the surface and resumes floating.
Q2. In what direction and at what point does the buoyant force on a body due to a liquid act?
Solution:
The centre of buoyancy is where a liquid’s buoyant force exerts upward on a body.
Q3. What is meant by the term buoyancy?
Solution:
The ability of a liquid to pull a person submerged in it higher is known as buoyancy.
Q4. Define upthrust and state its S.I. unit.
Solution:
The term “upthrust” refers to the upward push that a body experiences while submerged in a fluid. Newton is its SI unit.
Q5. What is the cause of upthrust? At which point can it be considered to act?
Solution:
Pressure is applied by a liquid inside a vessel in all directions and at all locations. In a liquid, the pressure at a given place is constant in all directions—upward, downward, and sideways. With increasing liquid depth, it rises. The thrusts operating on the side walls of a body are neutralised when it is submerged in a liquid because they are equivalent in size and directed in the opposite direction. The pressure levels on the top and lower faces, however, are not equal. A net upward force (=pressure x area) or upthrust is produced on the body by the difference in pressure between the top and lower faces. It controls buoyancy from the centre out.
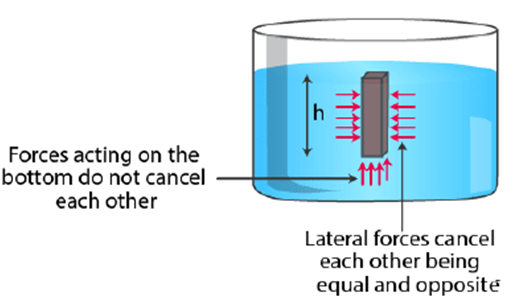
Q6. Why is a force needed to keep a block of wood inside water?
Solution:
When completely immersed, a block experiences an upward force greater than its weight. Since water has a greater density than cork, when a block of cork is completely submerged in water, the upthrust caused by water on the cork is greater than the weight of the block.
Q7. A piece of wood if left under water comes to the surface. Explain the reason.
Solution:
When left under water, a piece of wood rises to the surface because the upthrust caused by the submerged portion of the object equals the object’s own weight.
Q8. Describe an experiment to show that a body immersed in a liquid appears lighter than it really is.
Solution:
Experiment to show that a body immersed in a liquid appears lighter:
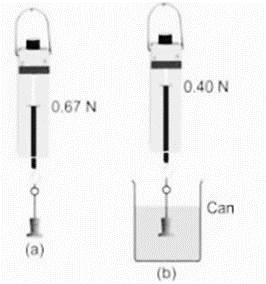
As indicated in the above illustration, take a solid object and suspend it using a tiny thread from the hook of a spring balance (a). Observe its weight. The weight is indicated in figure (a) above as 0.67 N. then gets a water-filled can. Hanging from the spring balance’s hook, slowly lower the solid into the water as illustrated in figure (b). Observe its weight. The weight is indicated in figure (b) above as 0.40 N. This example (breading)’s must be lower than case (a’s reading), demonstrating that a body submerged in liquid seems to be lighter.
Q9. Will a body weigh more in air or vacuum when weighed with a spring balance? Give a reason for your answer.
Solution:
A body should weigh more when it is in a vacuum since there is no upthrust acting on the body when there is no air there.
Q10. A metal solid cylinder tied to a thread is hanging from the hook of a spring balance. The cylinder is gradually immersed into the water contained in a jar. What changes do you expect in the readings of the spring balance? Explain your answer.
Solution:
The spring balance’s measurements decline. The cylinder experiences an upward force when it is submerged in the water-filled jar, which is in opposition to the cylinder’s weight. As a result, the cylinder seems lighter.
Q11. A body dipped into a liquid experiences an upthrust. State two factors on which upthrust on the body depend.
Solution:
Upthrust on a body depends on the following factors:
(i) The body’s volume submerged in the fluid.
(ii) The liquid or fluid’s density that the body is immersed in.
Q12. How is the upthrust related to the volume of the body submerged in a liquid?
Solution:
The upthrust operating on a body increases with the volume of the body submerged in the liquid.
Q13. A bunch of feathers and a stone of the same mass are released simultaneously in air. Which will fall faster and why? How will your observation be different if they are released simultaneously in vacuum?
Solution:
Due to air friction, when a group of feathers and a stone of the same mass are released simultaneously in the air, the feathers will drop after the stone. The feathers and the stone will descend at the same time in a vacuum since there is no air friction and consequently no difference in the acceleration caused by gravity for the two bodies.
Q14. A body experiences an upthrust F1 in river water and F2 in sea water when dipped up to the same level. Which is more, F1 or F2? Give reason.
Solution:
F2 > F1; Since sea water is denser than river water, its upthrust will be stronger at the same level than that of river water. The body will look lighter in the waters as a result of this.
Q15. A small block of wood is completely immersed in (i) water, (ii) glycerine and then released. In each case, what do you observe? Explain the difference in your observation in the two cases.
Solution:
Observation: A block of wood submerged in glycerine has a lower volume than a block submerged in water.
Reason: Glycerine has a higher density than water. In presence of light, the block of wood floats in glycerine with a smaller volume because glycerine exerts a greater upthrust on it than water does.
Q16. A body of volume V and density ρ is kept completely immersed in a liquid of density ρL. If g is the acceleration due to gravity, then write expressions for the following:
(i) The weight of the body,
(ii) The upthrust on the body,
(iii) The apparent weight of the body in liquid,
(iv) The loss in weight of the body.
Solution:
(i) Weight of the body = Vρg
(ii) Upthrust on the body = VρL g
(iii) Apparent weight of the body in liquid = V(ρ – ρL) g
(iv) Loss in weight of the body = V ρL g
Q17. A body held completely immersed inside a liquid experiences two forces:
(i) F1, the force due to gravity and
(ii) F2, the buoyant force.
Draw a diagram showing the direction of these forces acting on the body and state the condition when the body will float or sink.
Solution:
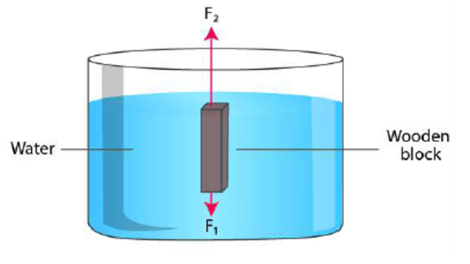
If F1 < F2 or F1 = F2, the body will float.
If F1 > F2, the body will sink.
Q18. Complete the following sentence:
(i) Two balls, one of iron and the other of aluminium experience the same upthrust when dipped completely in water if _____________
(ii) An empty tin container with its mouth closed has an average density equal to that of a liquid. The container is taken 2 m below the surface of that liquid and is left there. Then the container will ____________ .
(iii) A piece of wood is held under water. The upthrust on it will be ___________ the weight of the wood piece.
Sol:
(i) Two balls, one of iron and the other of aluminium experience the same upthrust when dipped completely in water if Both have equal volumes
(ii) An empty tin container with its mouth closed has an average density equal to that of a liquid. The container is taken 2 m below the surface of that liquid and is left there. Then the container will Remain at the same position.
(iii) A piece of wood is held under water. The upthrust on it will be More than the weight of the wood piece.
Q19. Prove that the loss in weight of a body when immersed wholly or partially in a liquid is equal to the buoyant force (or upthrust) and this loss is because of the difference in pressure exerted by liquid on the upper and lower surfaces of the submerged part of body.
Sol:
As seen in the above image, take into consideration a cylindrical body PQRS with a cross sectional area of A submerged in a liquid of density. Assume that the body’s lower surface RS is at a depth h2 below the liquid’s free surface and its upper surface PQ is at a depth h1.
At depth h1, the pressure on the upper surface PQ,
P1 = h1ρg
Therefore, the downward thrust on the upper surface PQ,
F1 = Pressure x Area = h1ρgA______________(i)
At depth h2, pressure on the lower surface RS,
P2 = h2 ρ g
Therefore, the upward thrust on the lower surface RS,
F2 = Pressure x Area = h2 ρ gA____________(ii)
The horizontal thrust at various points on the vertical sides of body get balanced because the liquid pressure is the same at all points at the same depth.
From the above equations (i) and (ii), it is clear that F2 > F1 because h2 > h1 and therefore, body will experience a net upward force.
Resultant upward thrust or buoyant force on the body,
FB = F2 – F1
FB = h2 ρ gA – h1 ρgA
FB = A (h2 – h1) ρ g
However, A (h2 – h1) = V, the volume of the body is submerged in a liquid.
Therefore, upthrust FB = V ρ g.
Now, Vρg = Volume of solid immersed x Density of liquid × Acceleration due to gravity
= Volume of liquid displaced x Density of liquid × Acceleration due to gravity
= Mass of liquid displaced x Acceleration due to gravity
= Weight of the liquid displaced by the submerged part of the body
Hence, Upthrust FB = weight of the liquid displaced by the submerged part of the body_____(iii)
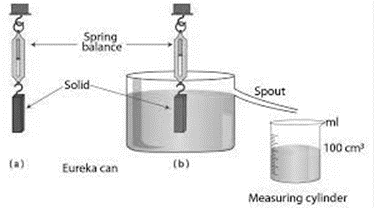
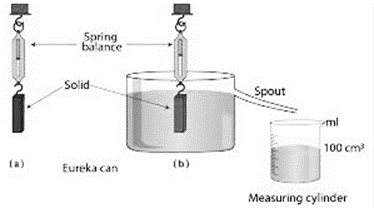
Now, let us take a solid and suspend it by a thin thread from the hook of a spring balance and note its weight. Then take a eureka can and fill it with water up to its spout. Arrange a measuring cylinder below the spout of the eureka can as shown. Immerse the solid gently in water. The water displaced by the solid is collected in the measuring cylinder.
When the water stops dripping through the spout, note the weight of the solid and volume of water collected in the measuring cylinder.
From the diagram, it is clear that
Loss in weight (Weight in air – Weight in water) = Volume of water displaced.
Loss in weight = Volume of water displaced × 1 gcm-3 [Because the density of water = 1gcm3]
Loss in weight = Weight of water displaced___________(iv)
From equations (iii) and (iv),
Loss in weight = Upthrust or buoyant force
Q20. A sphere of iron and another sphere of wood of the same radius are held under water. Compare the upthrust on the two spheres.
Solution:
The water will exert the same upthrust on both spheres since they have the same radius and hence the same volume inside the water. Hence, a 1:1 upthrust ratio between the two spheres is needed.
Q21. A sphere of iron and another of wood, both of same radius are placed on the surface of water. State which of the two will sink? Give a reason for your answer.
Solution:
Iron sphere will sink. Because iron has a higher density than water, its weight will be greater than the upthrust caused by water in it, causing the iron sphere to sink.
It is given that, wood has a lower density than water, the weight of a sphere made of wood should be less than the upthrust caused by water inside of it. The wood sphere will thus float because the amount of water inside it is balanced by the upthrust caused by the water.
Q22. How does the density of material of a body determine whether it will float or sink in water?
Solution:
In it, bodies with average densities higher than the liquid sink. While objects with typical densities that are equivalent to or less dense than liquid float atop it.
Q23. A body of density ρ is immersed in a liquid of density ρL. State the condition when the body will (i) float and (ii) sink in the liquid.
Solution:
(i) The body float if ρ < or = ρL.
(ii) The body sink if ρ > ρL.
Q24. It is easier to lift a heavy stone under water than in air. Explain.
Solution:
Under water, it is simpler to raise a heavy stone because the upward force of the water decreases the stone’s apparent weight and making lifting it easier.
Q25. State the Archimedes’ principle.
Solution:
According to Archimedes’ principle, a body that is partially or totally submerged in a liquid will feel an upthrust that is equivalent to the weight of the liquid that it has displaced.
Q26. Describe an experiment to verify the Archimedes’ principle.
Solution:
Experiment to verify Archimedes’ principle:
a) Suspend a solid from the spring balance’s hook using a fine thread. Note the object’s weight.
b) Up to the spout, fill a eureka can with water. As shown in the diagram, place a measuring cylinder beneath the eureka’s spout. Gently immerse the solid in the water, then gather the water that has been spread out in the measuring cylinder.
c) Once the water stops dripping down the spout, weigh the solid and measure the volume of water that has accumulated in the measuring cylinder.
d) The graphic makes it evident that the volume of the water displaced equals the difference between the weights of air and water, i.e.,
Volume of water = Weight in air – weight in water
• 300gf – 200gf = 100gf
• The volume of water expended is equal to the volume of solid, or 100 cm3.
• Given that water has a density of 1 g cm-3
• The weight of the water expelled is equal to the weight loss or upthrust, which is equal to 100gf.
EXERCISE-5A
MULTIPLE CHOICE TYPES
Q1. A body will experience minimum upthrust when it is completely immersed in:
a) Turpentine
b) Water
c) Glycerine
d) Mercury
Solution: a) Turpentine
Q2. The S.I. unit of upthrust is:
a) Pa
b) N
c) kg
d) kg m2
Solution: b) N
Q3. A body of density ρ sinks in a liquid of density ρL. The densities ρ and ρL are related as:
a) ρ = ρL
b) ρ < ρL
c) ρ > ρL
d) Nothing can be said.
Solution: c) ρ > ρL
EXERCISE-5A
Q1. A body of volume 100 cm3 weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8 x 103 kg m-3. Find:
(i) The upthrust due to liquid and
(ii) The weight of the body in liquid.
Sol:
Volume of body = V= 100 cm3= m100×10-6= 10-4 m3
Weight in air W = 5 kgf
Density of liquid d = kg/m1.8×103 kg/m3
(i) Upthrust due to liquid = Volume of the solid submerged × density 0
Upthrust due to liquid = g 10-4×1.8×103×g
Upthrust due to liquid = 0.18 gN
Upthrust due to liquid = 0.18 kgf
(ii) Weight of body in liquid = Weight of body in air – upthrust
Weight of body in liquid = 5 kgf – 0.18 kgf
Weight of body in liquid = 4.82 kgf
Q2. A body weighs 450 gf in air and 310 gf when completely immersed in water. Find
(i) The volume of the body,
(ii) The loss in weight of the body, and
(iii) The upthrust on the body.
State the assumption made in part (i).
Sol:
Weight of body in air = 450gf
Weight of body in water = 310gf
(i) Volume of the body = Loss in weight × density of water
Volume of the body = (450 – 310) × 1 (density of water = 1 gcm3
Volume of the body = 140 cm3
(ii) Loss in weight = Weight of body in air – Weight of body water
Loss in weight = (450 – 310)gf
Loss in weight = 140gf
(iii) Upthrust on body = loss in weight = 140gf

