Selina ICSE Class 10 Maths Solutions Chapter 14 Equation Of A Line

Question 1. Find, which of the following points lie on the line x – 2y + 5 = 0:
(i) (1, 3)
(ii) (0, 5)
(iii) (-5, 0)
(iv) (5, 5)
(v) (2, -1.5)
(vi) (-2, -1.5)
Solution:
(i) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = 1 and 𝑦 = 3
Put the value of x and y in given equation,
(1)– 2(3) + 5 = 0
1– 6 + 5 = 0
−5 + 5 = 0
0 = 0
Here, 𝐿𝐻𝑆 = 𝑅𝐻𝑆
Hence, the point (1,3) lies on the line 𝑥– 2𝑦 + 5 = 0.
(ii) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = 0 and 𝑦 = 5
Put the value of x and y in given equation,
(0)– 2(5) + 5 = 0
0– 10 + 5 = 0
−10 + 5 = 0
−5 = 0
𝐿𝐻𝑆 ≠ 𝑅𝐻𝑆
Hence, the point (0,5) does not lies on the line 𝑥– 2𝑦 + 5 = 0.
(iii) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = −5 and 𝑦 = 0
Put the value of x and y in given equation,
(−5)– 2(0) + 5 = 0
−5– 0 + 5 = 0
−5 + 5 = 0
0 = 0
𝐿𝐻𝑆 = 𝑅𝐻𝑆
Hence, the point (-5,0) lies on the line 𝑥– 2𝑦 + 5 = 0.
(iv) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = 5 and 𝑦 = 5
Put the value of x and y in given equation,
(5)– 2(5) + 5 = 0
5– 10 + 5 = 0
10 − 10 = 0
0 = 0
𝐿𝐻𝑆 = 𝑅𝐻𝑆
Hence, the point (5,5) lies on the line 𝑥– 2𝑦 + 5 = 0.
(v) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = 2 and 𝑦 = −1.5
Put the value of x and y in given equation,
(2)– 2(−1.5) + 5 = 0
2 + 3 + 5 = 0
10 = 0
𝐿𝐻𝑆 ≠ 𝑅𝐻𝑆
Hence, the point (2,-1.5) does not lies on the line 𝑥– 2𝑦 + 5 = 0.
(vi) Given that, the line is 𝑥– 2𝑦 + 5 = 0
Here, 𝑥 = −2 and 𝑦 = −1.5
Put the value of x and y in given equation,
(−2)– 2(−1.5) + 5 = 0
−2 + 3 + 5 = 0
6 = 0
𝐿𝐻𝑆 ≠ 𝑅𝐻𝑆
Hence, the point (-2,-1.5) does not lies on the line 𝑥– 2𝑦 + 5 = 0.

Question 2. State, true or false:
(i) The line x/2 + y/3 = 0 passes through the point (2,3).
(ii) The line x/2 + y/3 = 0 passes through the point (4,-6).
(iii) The point (8,7) lies on the line y – 7 = 0.
(iv) The point (-3,0) lies on the line x + 3 = 0.
(v) The point (2,a) lies on the line 2x – y = 3, then a = 5.
Solution:
(i) The given line is x/2 + y/3 = 0
Here, x = 2 and y = 3
Put the value of x and y in given equation,

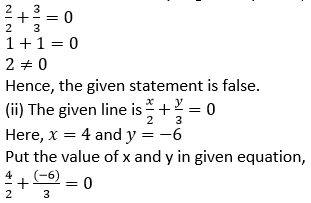
2 + (−2) = 0
0 = 0
Hence, the given statement is true.
(iii) The given line is 𝑦 − 7 = 0
Here, 𝑥 = 8 and 𝑦 = 7
Put the value of x and y in given equation,
7 − 7 = 0
0 = 0
Hence, the given statement is true.
(iv) The given line is 𝑥 + 3 = 0
Here, 𝑥 = −3 and 𝑦 = 0
Put the value of x and y in given equation,
−3 + 3 = 0
0 = 0
Hence, the given statement is true.
(v) The given line is 2𝑥 − 𝑦 = 3
Here, 𝑥 = 2 and 𝑦 = 𝑎
Put the value of x and y in given equation,
2(2) − 𝑎 = 3
4 − 𝑎 = 3
−𝑎 = 3 − 4
−𝑎 = −1
𝑎 = 1
Hence, the given statement is false.

Question 3. The line given by the equation 2x – y/3 = 7 passes through the point (k,6); calculate the value of k.
Solution:
It is given that, the equation 2x – y/3 = 7 passes through the point (k,6).
Here, x = k and y = 6
Put the value of x and y in given equation,
2(k) – 6/3 = 7
2(k) – 2 = 7
2k-2 = 7
2k = 7 + 2
2k = 9
k = 9/2
k = 4.5
Hence, the value of k is 4.5.

Question 4. For what value of k will the point (3,-k) lie on the line 9x + 4y = 3?
Solution:
It is given that, the equation of the line is 9x + 4y = 3.
Here, x =3 and y =-k
Put the value of x and y in given equation,
9(3) + 4(-k) =3
27 – 4k = 3
4k = 27 – 3
4k = 24
k = 24/4
k = 6
Hence, the value of k is 6.

Question 5. The line 3x/5-2y/3 + 1 = 0 contains the point (m,2m-1); calculate the value of m.
Solution:
It is given that, the equation is 3x/5 – 2y/3+1 = 0.
Here, x=m and y = 2m – 1
Put the value of x and y in given equation,

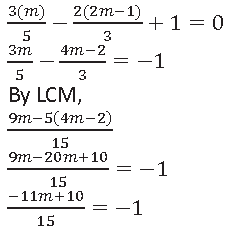
−11𝑚 + 10 = −1 × 15
−11𝑚 + 10 = −15
−11𝑚 = −15 − 10
−11𝑚 = −25
11𝑚 = 25
𝑚 = 25/11
𝑚 = 2(3/11)
Hence, the value of m is 2(3/11)
.
Question 6. Does the line 3x – 5y = 6 bisect the join of (5, -2) and (-1, 2)?
Solution:
It is given that, the line 3x – 5y = 6 bisect the join of (5, -2) and (-1, 2). The co-ordinates of the mid-point of AB are

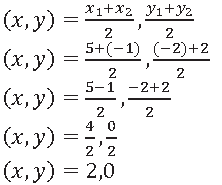
Put the value of x and y in given equation,
3x – 5y = 6
3(2) – 5(0) = 6
6 – 0 = 6
6 = 6
Hence, the line 3𝑥– 5𝑦 = 6 bisect the join of (5,-2) and (-1,2).

Question 7. (i) The line y = 3x – 2 bisects the join of (a, 3) and (2, -5), find the value of a.
(ii) The line x – 6y + 11 = 0 bisects the join of (8, -1) and (0, k). Find the value of k.
Solution:
(i) It is given that, the line 𝑦 = 3𝑥– 2 bisect the join of (a, 3) and (3, -5). The co-ordinates of the mid-point of AB are

Question 8. (i) The point (-3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
(ii) The line y = mx + 8 contains the point (-4, 4), calculate the value of m.
Solution:
(i) It is given that, the point (-3, 2) lies on the line ax + 3y + 6 = 0.
Here, 𝑥 = −3 and 𝑦 = 2
Put the value of x and y in given equation,
𝑎(−3) + 3(2) + 6 = 0
−3𝑎 + 12 = 0
3𝑎 = 12
𝑎 = 4
Hence, the value of a is 4.
(ii) It is given that, the line y = mx + 8 contains the point (-4, 4).
Here, 𝑥 = −4 and 𝑦 = 4
Put the value of x and y in given equation,
4 = −4𝑚 + 8
4𝑚 = 4
𝑚 = 1
Hence, the value of m is 1.

Question 9. The point P divides the join of (2, 1) and (-3, 6) in the ratio 2: 3. Does P lie on the line x – 5y + 15 = 0?
Solution:
It is given that, point P divides the join of (2, 1) and (-3, 6) in the ratio 2: 3. By section formula,

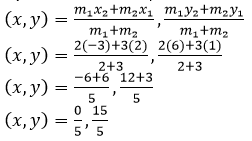
(𝑥, 𝑦) = 0,3
Here, 𝑥 = 0 and 𝑦 = 3
Put the value of x and y in given equation,
𝑥– 5𝑦 + 15 = 0
0– 5(3) + 15 = 0
0– 15 + 15 = 0
– 15 + 15 = 0
0 = 0
Hence, the point P lies on the line 𝑥– 5𝑦 + 15 = 0.

Question 10. The line segment joining the points (5,-4) and (2,2) is divided by the point Q in the ratio 1: 2. Does the line x – 2y = 0 contain Q?
Solution:
It is given that, point P divides the join of (5, -4) and (2, 2) in the ratio 1: 2. By section formula,

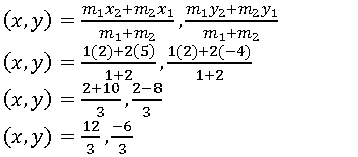
(x,y)=4,-2
Here, x=4 and y=-2
Put the value of x and y in given equation,
x – 2y = 0
4 – 2(-2) = 0
4 + 4 = 0
8 ≠ 0
Hence, the point Q does not lie on the line x – 2y = 0.

Question 11. Find the point of intersection of the lines:
4x + 3y = 1 and 3x – y + 9 = 0. If this point lies on the line (2k – 1)x – 2y = 4; find the value of k.
Solution:
It is given that,
4x + 3y = 1…..….(1)
3x – y + 9 = 0 ………(2)
From equation (1) we get, the value of x,
4x + 3y = 1

𝑥 = −2
Here, 𝑥 = −2 and 𝑦 = 3
Put the value of x and y in given equation,
(2𝑘– 1)𝑥– 2𝑦 = 4.
(2𝑘– 1)(−2)– 2(3) = 4
−4𝑘 + 2– 6 = 4
−4𝑘 = 8
𝑘 = −2
Hence, the value of k is -2.

Question 12. Show that the lines 2x + 5y = 1,x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Solution:
When two or more lines meet at a single location, they are said to be concurrent.
The point of intersection of the first two lines,
2𝑥 + 5𝑦 = 1 … . … . (1)
𝑥– 3𝑦 = 6 … … . . (2)
Form equation (2) we get the value of (2),
𝑥– 3𝑦 = 6
𝑥 = 6 + 3𝑦 … … … . (3)
Put the value of (3) in equation (1)
2𝑥 + 5𝑦 = 1
2(6 + 3𝑦) + 5𝑦 = 1
12 + 6𝑦 + 5𝑦 = 1
11𝑦 = 1 − 12
11𝑦 = −11
𝑦 = −1
Put the value of y in equation (3)
𝑥 = 6 + 3𝑦
𝑥 = 6 + 3(−1)
𝑥 = 6 − 3
𝑥 = 3
Hence, the point of intersection is (3, -1).
x + 5y + 2 = 0, then the given lines will be concurrent.
Here, x = 3 and y = -1
Put the value of x and y in equation 𝑥 + 5𝑦 + 2 = 0
𝑥 + 5𝑦 + 2 = 0
3 + 5(−1) + 2 = 0
5– 5 = 0
0 = 0
(3, -1) also lie on the third line.
Hence, the given lines are concurrent

Exercise 14B

Question 1. Find the slope of the line whose inclination is:
(i) 0°
(ii) 30°
(iii) 72°30’
(iv) 46°
Solution:
(i) tan 0°=0
(ii) tan 30°=1/√3
(iii) tan 72°30’=3.1716
(iv) tan 46°=1.0355

Question 2. Find the inclination of the line whose slope is:
(i) 0
(ii) √3
(iii) 0.7646
(iv) 1.0875
Solution:
(i) ta n⁡0° = 0
Ɵ = 0°
(ii) tan Ɵ = √3
Ɵ = 60°
(iii) tan Ɵ = 0.7646
Ɵ = 37° 24′
(iv) tan Ɵ =1.0875
Ɵ = 47° 24′

Question 3. Find the slope of the line passing through the following pairs of points:
(i) (-2, -3) and (1, 2)
(ii) (-4, 0) and origin
(iii) (a, -b) and (b, – a)
Solution:

Question 4. Find the slope of the line parallel to AB if:
(i) A = (-2, 4) and B = (0, 6)
(ii) A = (0, -3) and B = (-2, 5)
Solution:

Question 5. Find the slope of the line perpendicular to AB if:
(i) A = (0, -5) and B = (-2, 4)
(ii) A = (3, -2) and B = (-1, 2)
Solution:
(i) A = (0, -5) and B = (-2, 4)

Slop of the line perpendicular to AB = -1/Slope of AB
Slop of the line perpendicular to AB = -1/-1
Slop of the line perpendicular to AB = -1/-1
Slop of the line perpendicular to AB = 1

Question 6. The line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a). Find a.
Solution:
It is given that, the line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a).

According to question, lines are parallel,
1 = 𝑎−5/5
1 × 5 = 𝑎 − 5
5 = 𝑎 − 5
5 + 5 = 𝑎
𝑎 = 10
Hence, the value of a is 10.

Question 7. The line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.
Solution:
It is given that, the line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1)

By cross-multiplication,
-1(6) = 6(2 – a)
-6 =12 – 6a
6a = 12 + 6
a =18/6
a =3
Hence, the value of a is 3.

Question 8. Without using the distance formula, show that the points A (4, -2), B (-4, 4) and C (10, 6) are the vertices of a right-angled triangle.
Solution:
It is given that, the points are A(4,-2), B(-4,4) and C(10,6) are the vertices of a right-angled triangle.

Question 9. Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.
Solution:
It is given that, the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.

Question 10. (-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
Solution:
It is given that, A(-2, 4), B(4, 8), C(10, 7) and D(11, -5) are the vertices of a quadrilateral.
Let us assumed that, P, Q, R and S be the mid-points of AB, BC, CD and DA .

Question 11. Show that the points P (a, b + c), Q (b, c + a) and R (c, a + b) are collinear.
Solution:
It is given that, the points P (a, b + c), Q (b, c + a) and R (c, a + b).

Question 12. Find x, if the slop of the line joining (x,2) and (8,-11) is -3/4.
Solution:
It is given that, the slop of the line joining (x,2) and (8,-11) is (-3)/4.
Let us assumed that, A = (x,2) and B= (8,-11)

Question 13. The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slope of all its sides.

Slope of AB = 0. As the slope of any line parallel to x-axis is 0.
ΔABC is an equilateral triangle ∠A = 60°
Slope of AC = tan 60° = √3. As the slope of any line parallel to x-axis is 0.
Slope of BC = -tan 60° = −√3. As the slope of any line parallel to x-axis is 0.

Question 14. The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also find:
(i) the slope of the diagonal AC,
(ii) the slope of the diagonal BD.

Solution:
It is given that, the side AB of a square ABCD is parallel to the x-axis.
The slop of any line parallel to x-axis is 0.
Slope of AB = 0
According to figure,
AB | | CD
Slope of AB = Slope of CD = 0
BC is perpendicular to AB,
Slope of BC = −1/𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵
Slope of BC = −1/0
Slope of BC = not defined
AD is perpendicular to AB,
Slope of AD = −1/𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵
Slope of AD = −1/0
Slope of AD = not defined
(i) Diagonal of a square is 45°, Diagonal AC makes an angle of 45° with the positive direction of x-axis.
Slope of AC = tan45°
Slope of AC = 1
(ii) Diagonal of a square is 45°, Diagonal AC makes an angle of−45° with the positive direction of x-axis.
Slope of AC = tan (−45°)
Slope of AC = −1

Question 15. A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find:
(i) the slope of the altitude of AB,
(ii) the slope of the median AD, and
(iii) the slope of the line parallel to AC.
Solution:

Question 16. The slope of the side BC of a rectangle ABCD is 2/3. Find:
(i) the slope of the side AB.
(i) the slope of the side AD.
Solution:
(i) It is given that, the slope of the side BC of a rectangle ABCD is 2/3.
Here, BC is perpendicular to AB.

Q17. Find the slope and the inclination of the line AB if:
(i) A = (-3,-2) and B = (1,2)
(ii) A = (0,-√3) and B = (3,0)
(ii) A = (-1,2√3) and B = (-2,√3)
Solution:
(i) Co-ordinates of A (-3,-2) and B (1,2)

Question 18. The points (-3, 2), (2, -1) and (a, 4) are collinear. Find a.
Solution:
It is given that, points A(-3, 2), B(2, -1) and C(a, 4) are collinear.

Question 19. The points (K, 3), (2, -4) and (-K + 1, -2) are collinear. Find K.
Solution:
It is given that, the points A(K, 3), B(2, -4) and C(-K+1, -2) are collinear.

Question 20. Plot the points A (1, 1), B (4, 7) and C (4, 10) on a graph paper. Connect A and B, and also A and C. Which segment appears to have the steeper slope, AB or AC? Justify your conclusion by calculating the slopes of AB and AC.
Solution:

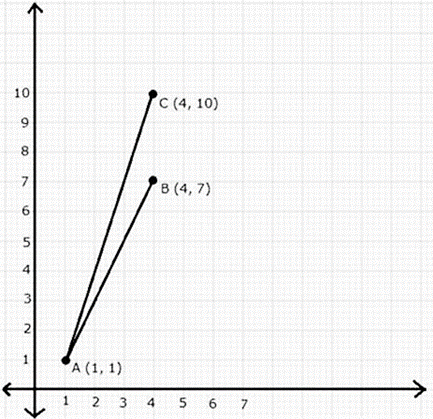
The formula of slope of the line = 𝑦₂−𝑦₁/𝑥₂−𝑥₁
Co-ordinates of A(1, 1) and B(4, 7)
Slope of AB = 7−1/4−1
Slope of AB = 6/3
Slope of AB = 2
Co-ordinates of A(1, 1) and C(4, 10)
Slope of AC = 10−1/4−1
Slope of AC = 9/3
Slope of AC = 3
We can say that, the line with greater slope is steeper.
Hence, AC has steeper slope.

Exercise 14C

Question 1. Find the equation of a line whose: y-intercept = 2 and slope = 3.
Solution:
It is given that, y-intercept c = 2 and slope m = 3
Substituting the values of c and m in the equation 𝑦 = 𝑚𝑥 + 𝑐
Hence, the required equation is 𝑦 = 3𝑥 + 2

Question 2. Find the equation of a line whose: y-intercept = -1 and inclination 𝟒𝟓°
Solution:
It is given that, y-intercept c = -1 and inclination = 45°
The slope of m is tan 45° = 1
Substituting the values of c and m in the equation 𝑦 = 𝑚𝑥 + 𝑐
Hence, the required equation is 𝑦 = 𝑥 − 1.

Question 3. Find the equation of the line whose slope is −4/3 and which passes through (-3, 4).
Solution:
It is given that, the slope is −4/3.
The equation passes through (-3,4) = (𝑥₁, 𝑦₁)
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 4 = −4
3 (𝑥 − (−3))
𝑦 − 4 = −4
3 (𝑥 + 3)
3(𝑦 − 4) = −4(𝑥 + 3)
3𝑦 − 12 = −4𝑥 − 12
4𝑥 + 3𝑦 = 0
Hence, the required equation is 4𝑥 + 3𝑦 = 0

Question 4. Find the equation of a line which passes through (5,4) and makes an angle of 𝟔𝟎° with the positive direction of the x-axis.
Solution:
The slope of the line tan60° is √3.
The equation passes through (5,4) = (𝑥₁, 𝑦₁)
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 4 = √3(𝑥 − 5)
𝑦 − 4 = √3𝑥 − 5√3
𝑦 = √3𝑥 − 5√3 + 4
Hence, the required equation is 𝑦 = √3𝑥 − 5√3 + 4.

Question 5. Find the equation of the line passing through:
(i) (0, 1) and (1, 2)
(ii) (-1, -4) and (3, 0).
Solution:
(i) The given co-ordinates of are (0, 1) and (1, 2)
The formula of slope of the line = 𝑦₂−𝑦₁/𝑥₂−𝑥₁
Slope of the line = 2−1/1−0
Slope of the line = 1/1
Slope of the line = 1
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 1 = 1(𝑥 − 0)
𝑦 − 1 = 𝑥
𝑦 = 𝑥 + 1
Hence, the required equation is 𝑦 = 𝑥 + 1.
(ii) The given co-ordinates of are (-1, -4) and (3, 0)

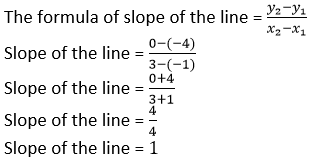
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − (−4) = 1(𝑥 − (−1))
𝑦 + 4 = 1(𝑥 + 1)
𝑦 + 4 = 𝑥 + 1
𝑦 = 𝑥 − 3
Hence, the required equation is 𝑦 = 𝑥 − 3

Question 6. The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find:
(i) the gradient of PQ;
(ii) the equation of PQ;
(iii) the co-ordinates of the point where PQ intersects the x-axis.
Solution:
(i) It is given that, the co-ordinates of two points P and Q are (2, 6) and (-3, 5)

(ii) The equation of PQ,
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 6 = 1
5 (𝑥 − 2)
5(𝑦 − 6) = 𝑥 − 2
5𝑦 − 30 = 𝑥 − 2
5𝑦 − 𝑥 = −2 + 30
5𝑦 − 𝑥 = 28
5𝑦 = 28 + 𝑥
Hence, the required equation is 5𝑦 = 28 + 𝑥.
(iii) Let us assumed that, the co-ordinates of the point where PQ intersects the x-axis at point 𝐴(𝑥, 0).
Put the value of 𝑦 = 0 in the above equation.
5𝑦 = 28 + 𝑥
5(0) = 28 + 𝑥
0 = 28 + 𝑥
𝑥 = −28
Hence, the value of x is -28.

Question 7. The co-ordinates of two points A and B are (-3, 4) and (2, -1). Find:
(i) the equation of AB;
(ii) the co-ordinates of the point where the line AB intersects the y-axis.
Solution:
(i) It is given that, co-ordinates of two points A and B are (-3,4) and (2,-1).
The formula of slope of the line = 𝑦₂−𝑦₁/𝑥₂−𝑥₁
Slope of the line = −1−4/2+3
Slope of the line = −5/5
Slope of the line = −1
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − (−1) = −1(𝑥 − 2)
𝑦 + 1 = −1(𝑥 − 2)
𝑦 + 1 = −𝑥 + 2
𝑦 + 1 = −𝑥 + 2
𝑥 + 𝑦 = 2 − 1
𝑥 + 𝑦 = 1
(ii) Let us assumed that, the co-ordinates of the point where AB intersects the y-axis at point 𝐴(0, 𝑦).
Put the value of 𝑥 = 0 in the above equation.
𝑥 + 𝑦 = 1
0 + 𝑦 = 1
𝑦 = 1
Hence, the value of y is 1.

Question 8. The figure given below shows two straight lines AB and CD intersecting each other at point P(3,4). Find the
equation of AB and CD.

Solution:
It is given that, the angle is 45°
Slope of line AB = 𝑡𝑎𝑛 45°
Slope of line AB = 1
The line AB passes through P(3,4).
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 4 = 1(𝑥 − 3)
𝑦 − 4 = 𝑥 − 3
𝑦 = 𝑥 − 3 + 4
𝑦 = 𝑥 + 1
Again,
The angle is 60°
Slope of line CD = 𝑡𝑎𝑛 60°
Slope of line CD = √3
The line AB passes through P(3,4).
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 4 = √3(𝑥 − 3)
𝑦 − 4 = 𝑥√3 − 3√3
𝑦 = 𝑥√3 − 3√3 + 4

Question 9. In ΔABC, A = (𝟑, 𝟓), B = (7, 8) and 𝑪 = (1, −10). Find the equation of the median through A.
Solution:
It is given that, the vertices of ΔABC, A = (3, 5), B = (7, 8) and C = (1, − 10).

Slope of the line = −6
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 5 = −6(𝑥 − 3)
𝑦 − 5 = −6𝑥 + 18
6𝑥 + 𝑦 = 18 + 5
6𝑥 + 𝑦 = 18 + 5
6𝑥 + 𝑦 = 23

Question 10. The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7,5). Find the equations of BC and CD.

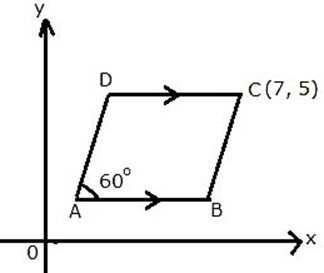
Solution:
It is given that, ABCD is a parallelogram.
∠A + ∠B = 180°
60° + ∠B = 180°
∠B = 180° − 60°
∠B = 120°
Slope of line CD = tan 60°
Slope of line CD = tan (90° + 30°)
Slope of line CD = cot 30°
Slope of line CD = √3
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 5 = √3(𝑥 − 7)
𝑦 − 5 = √3𝑥 − 7√3
𝑦 = √3𝑥 − 7√3 + 5
It is given that, AB is parallel to the x-axis.
CD||AB
Slope of line AB = 0
Slope of line AB = Slope of line CD
Substitution the values in 𝑦 − 𝑦₁ = m(𝑥 − 𝑥₁)
𝑦 − 5 = 0(𝑥 − 7)
𝑦 − 5 = 0
𝑦 = 5

Question 11. Find the equation of the straight line passing through origin and the point of intersection of the lines X + 2Y = 7 and X– Y = 4.
Solution:
It is given that, the point of intersection of the lines 𝑥 + 2𝑦 = 7 and 𝑥– 𝑦 = 4.
𝑥 + 2𝑦 = 7 … … … . (𝑖)
𝑥– 𝑦 = 4 … … … . . (𝑖𝑖)
From equation (ii) get the value of x,
𝑥 = 4 + 𝑦 … … … . . (𝑖𝑖𝑖)
Put the value of x in equation (i)
(4 + 𝑦) + 2𝑦 = 7
4 + 𝑦 + 2𝑦 = 7
3𝑦 = 3
𝑦 = 3/3
𝑦 = 1
Put the value of y in equation (iii)
𝑥 = 4 + 1
𝑥 = 5
The required line passes through (0,0) and (5,1)
The formula of slope of the line = 𝑦₂−𝑦₁/𝑥₂−𝑥₁
Slope of the line = 1−0/5−0
Slope of the line = 1/5
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 0 = 1/5 (𝑥 − 0)
5𝑦 = 𝑥
5𝑦 = 𝑥
0 = 𝑥 − 5𝑦
𝑥 − 5𝑦 = 0

Question 12. In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
Solution:
It is given that, the co-ordinated of Δ𝐴𝐵𝐶 are (4,7), (-2,3) and (0,1).
Let us assumed that, AD is the median through vertex A

Slope of the line AD = 1
Substitution the values in 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1)
𝑦 − 2 = 1(𝑥 − (−1))
𝑦 − 2 = 1(𝑥 + 1)
𝑦 − 2 = 𝑥 + 1
𝑦 − 𝑥 = 1 + 2
𝑦 = 3 + 𝑥
Slope of the line AC = 1−7/0−4
Slope of the line AC = −6/−4
Slope of the line AC = 3/2
Substitution the values in 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1)
𝑦 − 3 = 3/2 (𝑥 − (−2))
2(𝑦 − 3) = 3(𝑥 + 2)
2𝑦 − 6 = 3𝑥 + 6
2𝑦 − 3𝑥 = 6 + 6
2𝑦 = 3𝑥 + 12

Question 13. A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Solution:
It is given that, The co-ordinates A(0, 3), B(4, 4) and C(8, 0).

Slope of line perpendicular to BC = 1
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 3 = 1(𝑥 − 0)
𝑦 = 𝑥 + 3
Hence, the required equation is 𝑦 = 𝑥 + 3

Question 14. Find the equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1,4) and (2, 3).
Solution:
Let us assumed that, the co-ordinates are A(1, 4), B(2,3) and C(-1,2)

Slope of line perpendicular to BC = 1
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 2 = 1(𝑥 − (−1))
𝑦 − 2 = (𝑥 + 1)
𝑦 − 2 = 𝑥 + 1
𝑦 = 𝑥 + 1 + 2
𝑦 = 𝑥 + 3
Hence, the required equation is 𝑦 = 𝑥 + 3

Question 15. Find the equation of the line, whose:
(i) x-intercept = 5 and y-intercept = 3
(ii) x-intercept = -4 and y-intercept = 6
(iii) x-intercept = -8 and y-intercept = -4
Solution:
(i) x-intercept = 5 and y-intercept = 3
x-intercept = 5 means corresponding point on x-axis is (5,0)
y-intercept = 3 means corresponding point on y-axis is (0,3)

5𝑦 = −3(𝑥 − 5)
5𝑦 = −3𝑥 + 15
5𝑦 + 3𝑥 = 15
Hence, the required equation is 5𝑦 + 3𝑥 = 15
(ii) x-intercept = -4 and y-intercept = 6
x-intercept = -4 means corresponding point on x-axis is (-4,0)
y-intercept = 6 means corresponding point on y-axis is (0,6)

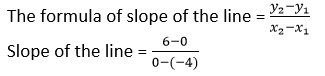
Slope of the line = 6/4
Slope of the line = 3/2
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 0 = 3
2 (𝑥 − (−4))
𝑦 = 3
2 (𝑥 + 4)
2𝑦 = 3𝑥 + 12
Hence, the required equation is 2𝑦 = 3𝑥 + 12
(iii) x-intercept = -8 and y-intercept = -4
x-intercept = -8 means corresponding point on x-axis is (-8,0)
y-intercept = -4 means corresponding point on y-axis is (0,-4)

Question 16. Find the equation of the line whose slope is −5/6 and x-intercept is 6.
Solution:
It is given that, x-intercept = 6 means corresponding point on x-axis is (6, 0).
Slope of the line = −5/6
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 0 = −5
6 (𝑥 − 6)
6𝑦 = −5(𝑥 − 6)
6𝑦 = −5𝑥 + 30
6𝑦 + 5𝑥 = 30

Question 17. Find the equation of the line with x-intercept 5 and a point on it (-3, 2).
Solution:
It is given that, x-intercept = 5 means corresponding point on x-axis is (-3, 2).

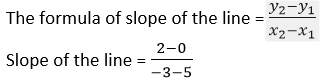
Slope of the line = 2/−8
Slope of the line = −1/4
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 0 = −1
4 (𝑥 − 5)
4𝑦 = −1(𝑥 − 5)
4𝑦 = −𝑥 + 5
4𝑦 + 𝑥 = 5
Hence, the required equation is 4𝑦 + 𝑥 = 5

Question 18. Find the equation of the line through (1, 3) and making an intercept of 5 on the y-axis.
Solution:
It is given that, y-intercept = 5 means corresponding point on y-axis is (0, 5).

Slope of the line = −2/1
Slope of the line = −2
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 5 = −2(𝑥 − 0)
𝑦 − 5 = −2(𝑥)
𝑦 − 5 = −2𝑥
𝑦 + 2𝑥 = 5
Hence, the required equation is 𝑦 + 2𝑥 = 5

Question 19. Find the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axis.
Solution:
Let us assumed that, AB and CD be two equally inclined lines.
Slope of line AB,
𝑡𝑎𝑛 45° = 1
(𝑥₁, 𝑦₁) = (−2,0)
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥1)
𝑦 − 0 = 1(𝑥 − (−2))
𝑦 = 1(𝑥 + 2)
𝑦 = 𝑥 + 2
Let us assumed that, AB and CD be two equally inclined lines.
Slope of line AB,
𝑡𝑎𝑛 − 45° = −1
(𝑥₁, 𝑦₁) = (−2,0)
Substitution the values in 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 0 = −1(𝑥 + 2)
𝑦 = −1(𝑥 + 2)
𝑦 = −𝑥 − 2
𝑦 + 𝑥 + 2 = 0

Question 20. The line through P(5,3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the co-ordinates of Q.

Solution:
(i) The equation of the y-axis is x = 0
It is given that the required line through P(5,3) intersects the y-axis at Q and the angle of inclination is 45˚.
Hence, the slope of line PQ = 𝑡𝑎𝑛 45° = 1
(ii) The equation of a line passing through the point A(𝑥1, 𝑦1) with slope ‘m’ is
The equation of the line passing through the point P(5,3) with slope 1 is
(𝑥1, 𝑦1) = (5,3)
Substitution the values in 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1)
𝑦 − 3 = 1(𝑥 − 5)
𝑦 − 3 = 𝑥 − 5
𝑦 − 𝑥 = −5 + 3
𝑦 − 𝑥 = −2
𝑥 − 𝑦 = 2
(iii) The equation of the line PQ is 𝑥 − 𝑦 = 2
It is given that, the line intersects with y-axis 𝑥 = 0.
Substituting 𝑥 = 0 in the equation 𝑥 − 𝑦 = 2
Put the value of 𝑥
0 − 𝑦 = 2
𝑦 = −2
Hence, the co-ordinates points of intersection Q are (0.-2).

Exercise 14D

Question 1. Find the slope and y-intercept of the line:
(i) y = 4
(ii) ax  –by = 0
(iii) 3x – 4y = 5
Solution:
(i) 𝑦 = 4
Substituting this equation with 𝑦 = 𝑚𝑥 + 𝑐
Slope of line = 0
Put the value of y in the above equation,
4 = 0𝑥 + 𝑐
4 = 𝑐
𝑐 = 4
y-intercept = c = 4
(ii) 𝑎𝑥– 𝑏𝑦 = 0
𝑎𝑥 = 𝑏𝑦
𝑎/𝑏 𝑥 = 𝑦
𝑦 = (𝑎/𝑏)𝑥
Substituting this equation with 𝑦 = 𝑚𝑥 + 𝑐
Slope of line = 𝑎/𝑏

Question 2. The equation of a line x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Solution:
It is given that, the equation of a line is 𝑥 − 𝑦 = 4
−𝑦 = 4 − 𝑥
𝑦 = 𝑥 − 4
Substituting this equation with 𝑦 = 𝑚𝑥 + 𝑐
Slope of line = 1
Slope of line = 1
y-intercept = c = -4
Let us assumed that, the inclination be Ɵ
Slope of line = 1
𝑡𝑎𝑛Ɵ = 𝑡𝑎𝑛45˚
Ɵ = 45˚
Hence, the inclination us 45˚.

Question 3. (i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
(ii) Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Solution:
(i) It is given that, 3𝑥 + 4𝑦 + 7 = 0
3𝑥 + 4𝑦 + 7 = 0
4𝑦 = −7 − 3𝑥

Slope of the line is 4/3
Hence, the product of the slope of the two lines is -1, the line are perpendicular to each other.
(ii) It is given that, 𝑥 − 3𝑦 = 4
−3𝑦 = −4 − 𝑥
−3𝑦 = −(4 + 𝑥)
3𝑦 = 𝑥 + 4
𝑦 = 1/3 𝑥 + 4/3
Slope of the line is 1/3
3𝑥– 𝑦 = 7
– 𝑦 = −3𝑥 − 7
𝑦 = 3𝑥 + 7
Slope of the line = 3
Product of slope of the two lines 11 ≠ −1
Hence, the lines are not perpendicular to each other.

Slope of the line = − 1/2
Product of slope of the two lines 3 ≠ −1
Hence, the lines are not perpendicular to each other.
(iv) It is given that, the slope of the line by (1,4) and (x,2) is 2.

By cross-multiplication,
2(𝑥 − 1) = −2
𝑥 − 1 = −1
𝑥 = −1 + 1
𝑥 = 0

Question 4. Find the slope of the line which is parallel to:
(i) x + 2y + 3 = 0

Solution.
(i) x + 2y + 3 = 0
2y = -x – 3

Question 5. Find the slope of the line which is perpendicular to:

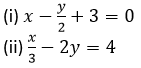
Solution:

By cross-multiplication,
y = 2(x + 3)
y = 2x + 6
Slope of the line = 2
Slope of the line which is perpendicular to given line = -1/Slope of the given line
Slope of the line which is perpendicular to given line = -1/2

Question 6. (i) Lines 2x – by + 3 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.
(ii) Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Solution:
(i) The given equation is 2x-by+3=0
2x + 3 = by
by = 2x + 3

Question 7. Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3p = 4 are perpendicular to each other.
Solution:
The given equation is 2𝑥 − 𝑦 + 5 = 0
−𝑦 = −7 − 2𝑥
𝑦 = 2𝑥 + 7
Slope of the line = 2
𝑝𝑥 + 3𝑦 = 4
3𝑦 = 4 − 𝑝𝑥
3𝑦 = −𝑝𝑥 + 4

Question 8. The equation of a line AB is 2x – 2y + 3 = 0.
(i) Find the slope of the line AB.
(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.
Solution:
(i) The given equation is 2𝑥– 2𝑦 + 3 = 0
– 2𝑦 = −2𝑥 − 3
2𝑦 = 2𝑥 + 3
𝑦 = 𝑥 + 3/2
Slope of the line = 1
(ii) Let the required angle be Ɵ
Slope of tan Ɵ = 1
tan Ɵ = tan 45˚
Ɵ = 45˚
Hence, the value of Ɵ is 45˚

Question 9. The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Solution:
The given equation is 4𝑥 + 3𝑦 = 9
3𝑦 = −4𝑥 + 9

Question 10. If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.
Solution:
The given equation is 𝑦 = 3𝑥 + 7
Slope of the line = 3
again,
2𝑦 + 𝑝𝑥 = 3
2𝑦 = −𝑝𝑥 + 3

Question 11. The line through A(-2,3) and B(4,b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
It is given that, the line through A(-2,3) and B(4,b) is perpendicular to the line 2x – 4y = 5

Question 12. Find the equation of the line through (-5, 7) and parallel to:
(i) x-axis
(ii) y-axis
Solution:
(i) The slope of the line parallel to x-axis is 0.
(𝑥₁, 𝑦₁) = (−5, 7)
Substituting this equation with 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 7 = 𝑚(𝑥 − (−5))
𝑦 − 7 = 𝑚(𝑥 + 5)
𝑦 − 7 = 0(𝑥 + 5)
𝑦 − 7 = 0
𝑦 = 7
Hence, the value of y is 7.
(ii) Here, the slope of the line parallel to y-axis in not defined. The slope of the line is tan90˚ and hence the given
line is parallel to y-axis.
(𝑥₁, 𝑦₁) = (−5, 7)
Required equation of the line is
𝑥 − 𝑥₁ = 0
𝑥 − (−5) = 0
𝑥 + 5 = 0

Question 13. (i) Find the equation of the line passing through (5, -3) and parallel to x – 3y = 4.
(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).
Solution:
(i) 𝑥 − 3𝑦 = 4
−3𝑦 = 4 − 𝑥
−3𝑦 = −(−4 + 𝑥)
3𝑦 = 𝑥 − 4

Slope of the line = 1/3
Required equation of the line passing through (5,-3)
Substituting this equation with 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)

3(𝑦 + 3) = 𝑥 − 5
3𝑦 + 9 = 𝑥 − 5
3𝑦 − 𝑥 = −5 − 9
3𝑦 − 𝑥 = −14
−(𝑥 − 3𝑦) = −14
𝑥 − 3𝑦 = 14
𝑥 − 3𝑦 − 14 = 0
(ii) 3𝑥 + 2𝑦 = 8
2𝑦 = 8 − 3𝑥
2𝑦 = −3𝑥 + 8

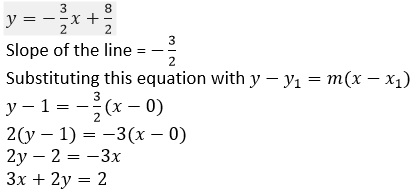
Question 14. Find the equation of the line passing through (-2, 1) and perpendicular to 𝟒𝒙 + 𝟓𝒚 = 𝟔.
Solution:
The given equation is 4𝑥 + 5𝑦 = 6
4𝑥 + 5𝑦 = 6
5𝑦 = −4𝑥 + 6

4(𝑦 − 1) = 5(𝑥 + 2)
4𝑦 − 4 = 5𝑥 + 10
4𝑦 − 5𝑥 = 14
5𝑥 − 4𝑦 = −14
5𝑥 − 4𝑦 + 14 = 0

Question 15. Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).
Solution:
Let the A(6,3) and B(0,3)
The perpendicular bisector of a line is perpendicular to the line and it bisects the line, that it, it passes through the mid-point of the line.

Question 16. In the following diagram, write down:
(i) the co-ordinates of the points A, B and C.
(ii) the equation of the line through A and parallel to BC.

Solution:
(i) The co-ordinates of point A, B and C are (2,3), (-1,2) and (3,0) respectively.

The equation of the line is 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 3 = −1/2 (𝑥 − 2)
2(𝑦 − 3) = −1(𝑥 − 2)
2𝑦 − 6 = −𝑥 + 2
𝑥 + 2𝑦 = 2 + 6
𝑥 + 2𝑦 = 8
Hence, the required line is 𝑥 + 2𝑦 = 8.

Question 17. B(-5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.
Solution:
We know that, in a rhombus diagonal bisect each other at right angle. Let O be the point of intersection of the diagonals AC and BD.

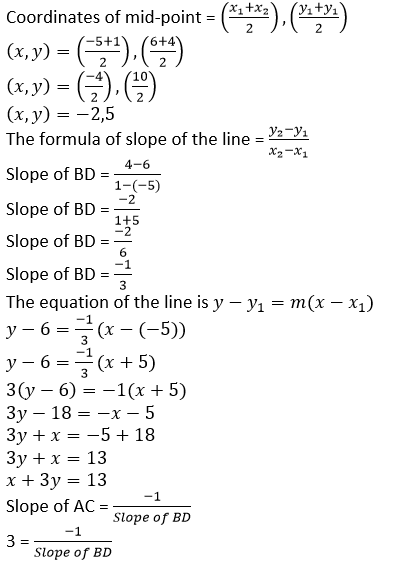
The equation of the line is 𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁)
𝑦 − 5 = 3(𝑥 − (−2))
𝑦 − 5 = 3(𝑥 + 2)
𝑦 − 5 = 3𝑥 + 6
𝑦 = 3𝑥 + 6 + 5
𝑦 = 3𝑥 + 11

Question 18. A = (7, -2) and C = (-1, -6) are the vertices of square ABCD. Find the equations of diagonal BD and of diagonal AC.
Solution:
In a square, diagonals bisect each other at right angle. Let O be the point of intersection of the diagonals AC and BD.

Slope of BD = −2
The equation of the line is 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1)
𝑦 − (−4) = −2(𝑥 − 3)
𝑦 + 4 = −2(𝑥 − 3)
𝑦 + 4 = −2𝑥 + 6
𝑦 + 2𝑥 = 6 − 4
2𝑥 + 𝑦 = 2

Question 19. A (1, -5), B (2, 2) and C (-2, 4) are the vertices of triangle ABC, find the equation of:
(i) the median of the triangle through A.
(ii) the altitude of the triangle through B.
(iii) the line through C and parallel to AB.
Solution:
(i) The median through A will pass through the mid-point of BC. Let AD be the median through A.

Slope of AB = −7
Slope of the line parallel to AB = Slope of AB = 7
The equation of the line is 𝑦 − 𝑦₁ = 𝑚(𝑥 − x₁)
𝑦 − 4 = 7(𝑥 − (−2))
𝑦 − 4 = 7(𝑥 + 2)
𝑦 − 4 = 7𝑥 + 14
𝑦 − 7𝑥 = 14 + 4
𝑦 − 7𝑥 = 18
Hence, the required equation is 𝑦 − 7𝑥 = 18.

Question 20. (i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
Solution:
(i) The given equation is 2𝑦 = 3𝑥 + 5

Question 21. Point P divides the line segment joining the points A (8, 0) and B (16, -8) in the ratio 3: 5. Find its coordinates of point P. Also, find the equation of the line through P and parallel to 3x + 5y = 7.
Solution:
It is given that, Point P divides the line segment joining the points A (8, 0) and B (16, -8) in the ratio 3: 5.