Selina ICSE Class 10 Maths Solutions Chapter 22 Heights And Distances

Exercise 22 A

Question 1. The height of a tree is √3 times the length of its shadow. Find the angle of elevation of the sun.
Solution:

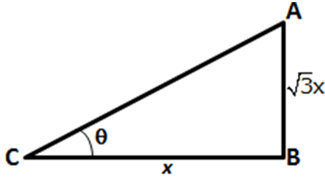
Let us assumed that, the length of the shadow of the tree be xm.
Height of the tree = √3 x
If Ɵ is the angle of elevation of the sun, then
tanƟ = √3x/x
tanƟ = √3
We know that, tan60˚ = √3
tanƟ = tan60˚
Ɵ = 60˚

Question 2. The angle of elevation of the top of a tower from a point on the ground and at a distance of 160 m from its foot, is found to be 60o. Find the height of the tower.
Solution:

Let us assumed that, height of the tower be hm. Also given that, angle of elevation is 60˚
tan60˚ = h/160
We know that, tan60˚ = √3
√3 = h/160
h = 160√3
h = 160×1.732
h = 277.12m
Hence, the height of the tower is 277.12m

Question 3. A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68˚ with the ground. Find the height, upto which the ladder reaches.
Solution:

Let us assumed that, the height upto which the ladder reaches be hm. Also given that the angle of elevation is 68˚.
tan68˚ = h/2.4
2.475 = h/2.4
h = 2.475×2.4
h = 5.94m

Question 4. Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30o and 38o respectively. Find the distance between them, if the height of the tower is 50 m.
Solution:

Let us assumed that, one person A be at a distance x and the second person B be at a distance of y from the foot of the tower. Also given that, angle of elevation of A is 30˚.
tan30˚ = 50/x
1/√3 = 50/x
x = 50√3
x = 50×1.732
x = 86.60m
The angle of elevation of B is 38˚
tan38˚ = 50/y
0.7813 = 50/y
y×0.7813 = 50
y = 50/0.7813
y = 64m
Hence, the distance of A and B is 86.60 + 64 = 150.6m

Question 5. A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30˚ with the ground.
Solution:

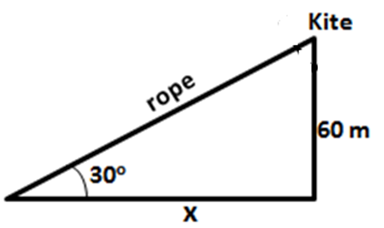
sin30˚ = 60/x
We know that, sin30˚ = 1/2
1/2 = 60/x
x = 60×2
x = 120m
Hence, the length of the rope is 120m.

Question 6. A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45˚, (ii) 60˚. Find the height of the tower in each case.
Solution:
(i) Let the height of the tower be hm.
It is given that, Ɵ = 45˚
tan45˚ = h – 1.6/20
We know that, tan45˚ = 1
tan45˚ = (h – 1.6)/20
1 = h – 1.6/20
1×20 = h – 1.6
20 = h – 1.6
h = 20 + 1.6
h = 21.6m
Hence, the height of the tower be 21.6m.
(ii) Let the height of the tower be hm.
It is given that, Ɵ = 45˚
tan60˚ = h – 1.6/20
We know that, tan60˚ = √3
√3 = (h – 1.6)/20
√3×20 = h – 1.6
1.732×20 = h – 1.6
34.64 = h – 1.6
h = 34.64 + 1.6
h = 36.24m
Hence, the height of the tower be 36.24m.

Question 7. The upper part of a tree, broken over by the wind, makes an angle of 45^o with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
Solution:
Let us assumed that, the height of the tree after breaking be hm.
It is given that, Ɵ = 45˚
tan45˚ = h/15
We know that, tan45˚ = 1
1 = h/15
h = 15m
Length of the tree broken by the wind = 15/(sin45˚) = 15√2
= 15×1.414
= 21.21m
Hence, the height of the tree before broken is 15 + 21.21 = 36.21m

Question 8. The angle of elevation of the top of an unfinished tower at a point distance 80m from its base is 30˚. How much higher must the tower be raised so that its angle of elevation at the same point may be 60˚?
Solution:

Let us assumed that, AB be the unfinished tower and C be the top of the tower when finished. Also P be a point 80m from the foot A.
In ΔBAP,
tan30˚ = AB/AP
We know that the value of tan30˚ = 1/√3
1/√3 = AB/80
AB = 80/√3
AB = 46.19m
In ΔCAP,
tan60˚ = AC/AP
We know that the value of tan60˚ = √3
tan60˚ = AC/AP
√3 = AC/80
AC = 80√3
AC = 138.56 m
Hence, the tower must be raised by 138.56 – 46.19 = 92.37m

Question 9. At a particular time, when the sun’s altitude is 30˚, the length of the shadow of a vertical tower is 45 m. Calculate
(i) the length of the tower.
(ii) the length of the shadow of the same tower, when the sun’s altitude is (a) 45˚ (b) 60˚.
Solution:
(i) Let us assumed that, the length of the tower be hm.
It is given that, Ɵ = 30˚
tan30˚ = h/45
We know that the value of tan30˚ = 1/√3

Question 10. Two vertical poles are on either side of a road. A 30m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32˚24′ with the pole and when it is turned to rest against another pole, it makes angle 32˚24′ with the road. Calculate the width of the road.
Solution:

Let us assumed that, AB be the ladder and ∠ABP = 32˚24’.
BP/AB = sin32˚24’
BP/30 = 0.536
BP = 0.536×30
BP = 16.08m
Let us assumed that, AC be the ladder and ∠CAQ = 32˚24’.
BQ/BC = cos32˚24’
BQ/30 = 0.844
BP = 0.844×30
BP = 25.32m
Hence, the width of the road is 16.08m + 25.32m = 41.4m.

Question 11. Two climbers are at points A and B on a vertical cliff face. To an observer C, 40m from the foot of the cliff, on the level ground, A is at an elevation of 48˚ and B of 57˚. What is the distance between the climbers?
Solution:

Let us assumed that, P be the foot of the cliff on level ground.
Then, ∠ACP = 48˚ and ∠BCP = 57˚
tan57˚ = BP/PC
we know that, tan57˚ = 1.539
1.539 = BP/40
BP = 40×1.539
BP = 61.57
tan48˚ = AP/PC
we know that, tan48˚ = 1.110
1.110 = AP/40
AP = 40×1.110
AP = 44.4m

Question 12. A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28˚ and the angle of depression of the bottom of the pole is 13˚. Calculate the height of the pole.
Solution:

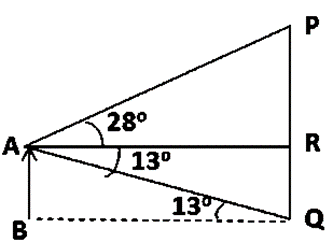
Let us assumed that, AB be the man and PQ be the flag-pole. Also given that AR = 9m, ∠PAR = 28˚ and ∠QAR = 13˚.
PR/AR = tan28˚
We know that, tan28˚ = 0.532
PR/9 = 0.532
PR = 0.532×9
PR = 4.788 m
For ∠QAR = 13˚
RQ/AR = tan13˚
We know that, tan13˚ = 0.231
RQ/9 = 0.231
RQ = 0.231×9
RQ = 2.079 m
Hence, the height of the pole is PR+RQ = 4.788+2.079 = 6.867m

Question 13. From the top of a cliff 92 m high, the angle of depression of a buoy is 20˚. Calculate, to the nearest meter, the distance of the buoy from the foot of the cliff.
Solution:

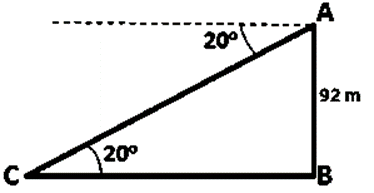
Let us assumed that, AB be the cliff and C be the buoy. Also given that AB = 92m. and ∠ACB = 20˚
tan20˚ = AB/BC
We know that, tan20˚ = 0.3640
0.3640 = 92/BC
BC = 92/0.3640
BC = 252.7m or 253m
Hence, the buoy is at a distance of 253m form the foot of the cliff.

Exercise 22 B

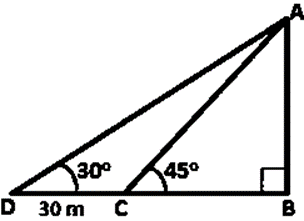
Question 1. In the figure, given below, it is given that AB is perpendicular to BD and is of length x metres. DC = 30m, ∠ADB = 30˚ and ∠ACB = 45˚. Without using table. Find x.

Solution:

Question 2. Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60 ˚ to 30˚.
Solution:

Let us assumed that, AB be the tree of height hm. CD = 20m, ∠ADB = 30˚ and ∠ACB = 60˚.
In ΔABC
tan60˚ = AB/BC
We know that, tan60˚ = √3

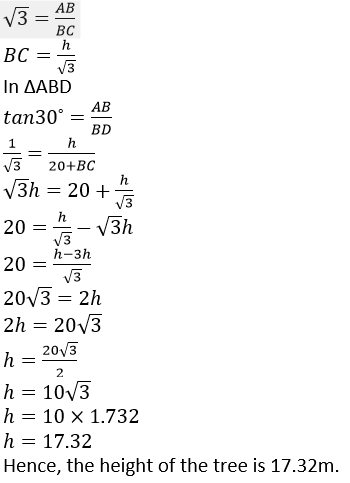
Question 3. Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30˚ to 45˚.
Solution:

Let us assumed that, AB be the building of height hm. Also two points be C and D such that CD = 40cm, ∠ADB = 30˚ and ∠ACB = 45˚
In ΔABC,
tan45˚ = AB/BC
We know that, tan45˚ = 1
1 = AB/BC
BC = AB = h
In ΔABD,
tan30˚ = AB/BD
We know that, tan30˚ = 1/√3
1/√3 = h/(40+h)
40+h = √3 h
40 = √3 h – h
√3 h – h = 40
h(√3 – 1) = 40
h(1.732 – 1) = 40
0.732h = 40
h = 40/0.732
h = 54.64m

Question 4. From the top of a light house 100 m high, the angles of depression of two ships are observed as 48˚ and 36˚ respectively. Find the distance between the two ships (in the nearest meter) if:
(i) the ships are on the same side of the light house.
(ii) the ships are on the opposite sides of the light house.
Solution:

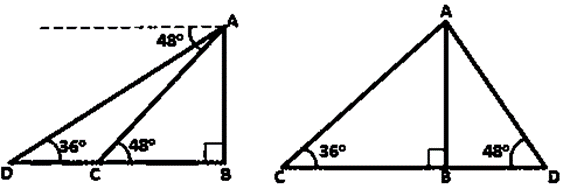
Let us assumed that, AB be the lighthouse and two ships be C and D such that ∠ADB = 36˚ and ∠ACB = 48˚.
In ΔABC,
tan48˚ = AB/BD
We know that, tan48˚ = 1.1106
tan48˚ = AB/BC
1.1106 = 100/BC
BC = 100/1.1106
BC = 90.04m
In ΔABD,
tan36˚ = AB/BD
We know that, tan36˚ = 0.7265
0.7265 = 100/BD
BD = 100/0.7265
BC = 137.64m
(i) If the ships are on the same side of the light house. Then distance between the two ships BD-BC = 48m
(ii) If the ships are on the opposite side of the light house. Then distance between the two ships BD+BC = 48m

Question 5. Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60˚ and 30˚; find the height of the pillars and the position of the point.
Solution:

Let us assumed that, AB and CD be the two towers of height h m. P be a point in the roadway BD such that BD = 150m.APB = 60˚ and ∠CPD = 30˚.
In ΔABP,
tan60˚ = AB/BP
We know that, tan60˚ = √3
√3 = h/BP
BP = h/√3
In ΔCDP,
tan30˚ = CD/DP
We know that, tan30˚ = 1/√3

h=64.95m
So, the height of the pillars is 64.95m. The point is BP/√3 from the first pillar. That is the position of the point is 64.95/√3 from the first pillar. This is the position of the point is 37.5m from first pillar.

Question 6. From the figure, given below, calculate the length of CD.

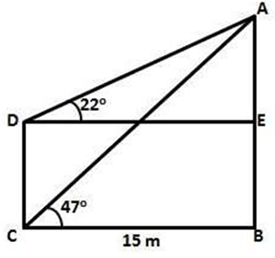
Solution:
In ΔAED
tan22˚ = AE/DE
We know that, tan22˚ = 0.404
0.404 = AE/15
AE = 15×0.404
AE = 6.06m
In ΔABC
tan47˚ = AB/BC
We know that, tan47˚ = 1.072
1.072 = AB/15
AB = 15×1.072
AB = 16.09m
CD = BE
= AB – AE
= 16.09 – 6.06
= 10.03m

Question 7. The angle of elevation of the top of a tower is observed to be 60˚. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45˚. Find:
(i) the height of the tower,
(ii) its horizontal distance from the points of observation.
Solution:

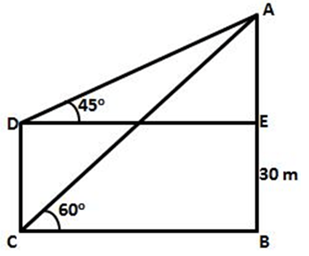
(i) In ΔABC,
tan60˚ = AB/BC
We know that tan60˚ = √3
tan60˚ = AB/BC
√3 BC = AB
√3 BC = AE + 30
√3 BC = BC + 30
√3 BC-BC = 30
BC(√3-1) = 30
BC = 30/√3 – 1
BC = 30/1.732 – 1
BC = 30/0.732
BC = 40.98m
AB = 30 + 40.98
AB = 70.98
So, the height of the tower is 70.98m.

(ii) The distance from the point of observation is BC = 40.98m

Question 8. From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30˚ and 60˚. Find the height of the tower.
Solution:

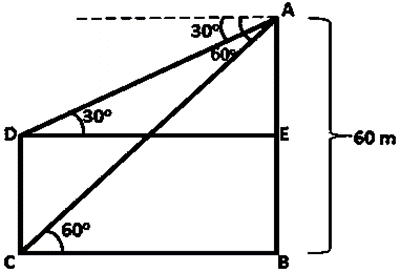
In ΔADE,
tan30˚ = AE/DE
We know that tan30˚ = 1/√3

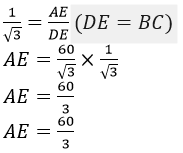
AE = 20
CD = EB
= AB-AE
= 60-20
= 40m
So, the height of the tower is 40˚m.

Question 9. A man on a cliff observes a boat, at an angle of depression 30˚, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60˚. Assuming that the boat sails at a uniform speed, determine:
(i) how much more time it will take to reach the shore.
(ii) the speed of the boat in metres per second, if the height of the cliff is 500 m.
Solution:

Let us assumed that, AB be the cliff and C and D be the two positions of the boat such that ∠ADE = 30˚ and ∠ACB = 60˚, speed of the boat be x meter per minute and let the boat reach the shore after t minutes more.
CD = 3xm and BC = txm
In ΔABC,
tan60˚ = AB/BC
We know that, tan60˚ = √3
√3 = h/tx
In ΔADB,
tan30˚ = AB/DB
We know that, tan30˚ = 1/√3

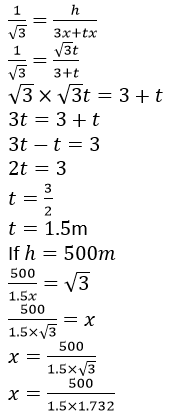
x = 192.45 metre/minute = 3.21m/sec
So, the boat takes an extra 1.5 minutes to reach the shore and the height of cliff is 500m, the speed of the boat is 3.21 m/sec.

Question 10. A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60˚ to 45˚. Find the speed of the boat.
Solution:

Let us assumed that, AB be the lighthouse and C and D be the two positions of the boat such that AB = 150m, ∠ADB = 45˚ and ∠ACB = 60˚ and Speed of the boat be x metre per minute.
Here, CD = 2xm
In ΔADB,
tan45˚ = AB/DB
We know that, tan45˚ = 1
1 = 150/DB
DB = 150m
In ΔABC,
tan60˚ = AB/BC
We know that, tan60˚ = √3

Question 11. A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60˚. When he moves 40 m away from the bank, he finds the angle of elevation to be 30˚. Find:
(i) the height of the tree, correct to 2 decimal places,
(ii) the width of the river.
Solution:

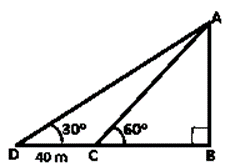
Let us assumed that, AB be the tree of height hm and BC be the width of the river. D be the point on the opposite bank of tree such that CD = 40m.
Here ∠ADB = 30˚ and ∠ACB = 60˚
In ΔABC,
tan60˚ = AB/BC
We know that, tan60˚ = √3
√3 = h/BC
h = BC√3
In ΔADB,
tan30˚ = AB/BD
We know that, tan30˚ = 1/√3

40 + BC = BC√3×√3
40 + BC = 3BC
40 = 2BC
BC = 40/2
BC = 20m
h = 20×1.732
h = 34.64m
So, height of the tree is 34.64m and width of the river is 20m.

Question 12. The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45˚. Find the height of the first tower.
Solution:

Let us assumed that, AB and CD be the two towers. The height of the first tower is AB = 160m. The horizontal distance between the two tower is BD = 75m.
The angle of depression of the first tower as seen from the top of the second tower is ∠ACE = 45˚.
In ΔACE,
tan45˚ = AE/EC
1 = AE/EC
EC = AE
EC = AE = BD = 75m
CD = EB
= AB-AE
= 160-75
= 85m
So, the height of the tower is 85m.

Question 13. The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30˚ than when it was 45˚. Prove that the height of the tower is y(√3+1) metres.
Solution:

Let us assumed that, AB be the tower and C and D are two points such that CD = 2ym, ∠ADB = 45˚ and ∠ACB = 30˚.
In ΔABD,
tan45˚ = AB/BD
We know that, tan45˚ = 1
1 = h/BD
BD = h
In ΔABC,
tan30˚ = AB/BC
We know that, tan30˚ = 1/√3
In ΔABC,
tan30˚ = AB/BD
We know that, tan30˚ = 1/√3
1/√3 = h/BC
BC = √3 h
CD + h = √3 h
2y = √3 h – h
2y = h(√3 – 1)

Question 14. An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60˚. After 10 seconds, its elevation is observed to be 30˚; find the uniform speed of the aeroplane in km per hour.
Solution:

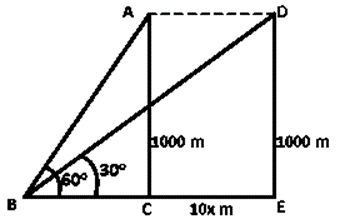
Let us assumed that, A be the aeroplane and B be the observer on the ground. The vertical height will be AC = 1km = 1000m. After 10seconds, let the aeroplane be at point D. Let the speed of the aeroplane be xm/sec.
Here, CE = 10x
In ΔABC,
tan60˚ = AC/BC
We know that, tan60˚ = √3

x = 100×1.154
x = 115.4m/sec
x = 115.4×18/5km/hr
x = 415.67km/hr
So, speed of the aeroplane us 415.67km/hr.

Question 15. From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30˚ and 45˚ respectively. Find the distances of the two stones from the foot of the hill.
Solution:

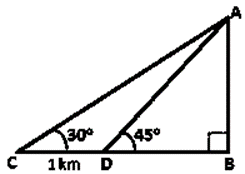
Let us assumed that, AB be the hill of height ‘h’km and C and D be the two consecutive stones such that CD = 1km, ∠ACB = 30˚ and ∠ADB = 45˚.
In ΔABD,
tan45˚ = AB/BD
We know that, tan45˚ = 1
1 = h/BD
BD = h
In ΔABC,
tan30˚ = AB/BC
We know that, tan30˚ = 1/√3

h = 1.366km
BD = 1.366km
BC = BD + DC
BC = 1.366 + 1
BC = 2.366km
So, the two stones are at a distance of 1.366km and 2.366km from the foot of the hill.