Selina ICSE Class 10 Maths Solutions Chapter 4 Linear Inequations In One Variable

Exercise 4A

Question 1. State, true or false:

(i) x<- y ⇒ – x >y

(ii) -5 x ≥ 15 ⇒ x ≥ – 3

(iii) 2 x ≤- 7 ⇒ 2 x /(-4) ≥ (-7)/(-4)

(iv) 7 > 5 ⇒ 1/7< 1/5

Question 2. State, whether the following statements are true or false:

(i) a < b, then a – c < b – c

(ii) If a > b, then a + c > b + c

(iii) If a < b, then ac > bc

(iv) If a > b, then a/c < b/c

(v) If a – c > b – d, then a + d > b + c

(vi) If a < b, and c > 0, then a – c > b – c
Where a, b, c and d are real numbers and c ≠ 0.

Question 3. If 𝒙 ∈ 𝑵, find the solution set of in equations.
(i) 𝟓𝒙 + 𝟑 ≤ 𝟐𝒙 + 𝟏𝟖
(ii) 𝟑𝒙– 𝟐 < 𝟏𝟗– 𝟒𝒙
Solution:
(i) 5𝑥 + 3 ≤ 2𝑥 + 18
5𝑥– 2𝑥 ≤ 18 – 3
3𝑥 ≤ 15
𝑥 ≤ 15/3
𝑥 ≤ 5
Hence, {1, 2, 3, 4, 5} is the solution set.
(ii) 3𝑥– 2 < 19– 4𝑥
3𝑥 + 4𝑥 < 19 + 2
7𝑥 < 21
𝑥 < 21/7
𝑥 < 3
Hence, {1, 2} is the solution set.

Question 4. If the replacement set is the set of whole numbers solve:
(i) x + 7 ≤ 11
(ii) 3x – 1 > 8
(iii) 8 – x > 5
(iv) 7- 3x ≥ – 1/2
(v) x – 3/2 < 3/2 – x
(vi) 18 ≤ 3x – 2
Solution :
(i) x + 7 ≤ 11
x ≤ 11 – 7
x ≤ 4
Hence, the set of whole number is {0, 1, 2, 3, 4}.
(ii) 3x – 1 > 8
3x > 8 + 1
3x > 9
x > 9/3
x > 3
Hence, the set of whole number is {4, 5, 6, …..}.
(iii) 8 – x > 5
– x > 5 –8
– x > – 3
x < 3
Hence, the set of whole number is {0, 1, 2}.
(iv) 7 – 3x ≥ – 1/2
– 3x ≥ – 1/2 – 7
– 3x ≥ – 1/2 – 7/1
– 3x ≥ ( – 1 – 14)/2
– 3x ≥ – 15/2
x ≥ 15/(2×3)
x ≤ 5/2
Hence, the set of whole number is {0, 1, 2}.
(v) x – 3/2 < 3/2 – x
x + x < 3/2 + 3/2
x + x < 3/2 + 3/2
2x < (3 + 3)/2
2x < 6/2
x < 3/2
Hence, the set of whole number is {0, 1}
(vi) 18 ≤ 3x – 2
18 + 2 ≤ 3x
20 ≤ 3x
x ≥ 20/3
Hence, the set of whole number is {7, 8, 9, …}

Question 5. Solve the in-equation:
3 – 2x ≥ x – 12 given that x ∈ N.
Solution :
3 – 2x ≥x – 12
-2x – x ≥ -12 – 3
-3x ≥ – 15
x ≥ 15/3
x ≤ 5
Hence, the set of solutions is {1, 2, 3, 4, 5}

Q5. Solve the in – equation:
3 – 2x ≥ x – 12 given that x ∈ N. 
Solution:
3 – 2x ≥ x – 12
– 2x – x ≥ – 12 – 3
– 3x ≥ – 15
x ≥ 15/3
x ≤ 5
Hence, the set of solutions is {1, 2, 3, 4, 5}

Question 6. If 25 – 4x ≤ 16, find:
(i) the smallest value of x, when x is a real number,
(ii) the smallest value of x, when x is an integer. 
Solution:
25 – 4x ≤ 16
– 4x ≤ 16 – 25
– 4x ≤ – 9
x ≥ 9/4
x ≥ 2.25
(i) The smallest value of x, when x is a real number is 2.25.
(ii) The smallest value of x, when x is an integer is 3.

Question 7. If the replacement set is the set of real numbers solve:
(i) – 4x ≥ – 16
(ii) 8 – 3x ≤ 20

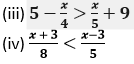
Solution:
(i) – 4x ≥ – 16
x ≤ 16/4
x ≤ 4
Hence, the replacement set is the set of real numbers is {x x ∈ R and x ≤ 4}.

(ii) 8 – 3x ≤ 20
– 3x ≤ 20 – 8
– 3x ≤ 12
– x ≤ 12/3
x ≥ – 4
Hence, the replacement set is the set of real numbers is {x x ∈ R and x ≥ – 4}

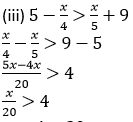
x > 4 × 20
x > 80
Hence, the replacement set is the set of real numbers is {x x ∈ R and x > 80}.

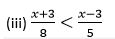
5(x + 3) < 8(x – 3)
5x + 15 < 8x – 24
5x – 8x < – 24 – 15
– 3x < – 39
x > 13
Hence, the replacement set is the set of real numbers is {x x ∈ R and x >13}.

Question 8. Find the smallest value of x for which 5 – 2x < 5 1/2 – 5/3 x, where x is an integer.
Solution

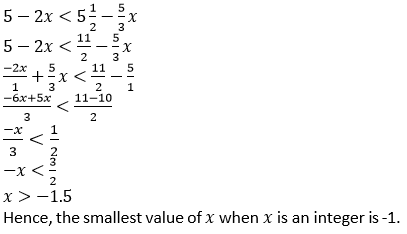
Question 9. Find the largest value of x for which 2(x–1) ≤ 9 – x and x ∈ W.
Solution:
2(x – 1) ≤ 9 – x
2x – 2 ≤ 9 – x
2x + x ≤ 9 + 2
3x ≤ 11
x ≤ 11/3
x ≤ 3.67
Hence, the largest value of x is 3 when x ∈ W.

Q10. Solve the in-equation: 12 + 1 5/6 x ≤ 5 + 3x and x ∈ R.
Solution 10. Solve the in-equation: 12 + 1 5/6 x ≤ 5 + 3x and x ∈ R.
Solution:

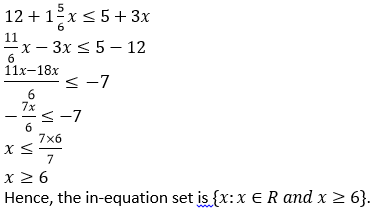
Question 11. Given x∈{integers}, find the solution set of: – 5 ≤ 2x – 3 < x + 2.
Solution:
– 5 ≤ 2x – 3 < x + 2
– 5 ≤ 2x – 3 and 2x – 3 < x + 2
– 5 + 3 ≤ 2x and 2x – x < 2 + 3
– 2 ≤ 2x and x < 5
2x ≥ – 2 and x < 5
x ≥ – 1 and x < 5
Hence, x∈{integers}, find the solution set is { – 1,0,1,2,3,4}.

Question 12. Given x∈{whole numbers}, find the solution set of: – 1 ≤ 3 + 4x < 23.
Solution:
– 1 ≤ 3 + 4x < 23
– 1 ≤ 3 + 4x and 3 + 4x < 23
– 1 – 3 ≤ 4x and 4x < 23 – 3
– 4 ≤ 4x and 4x < 20
– 1 ≥ x and x < 5
x ≥ – 1 and x < 5
Hence, the solution set is {0, 1, 2, 3, 4}.

Exercise 4B

Question 1. Represent the following inequalities on real number lines:
(i) 2x – 1 < 5
(ii) 3x + 1 ≥ – 5
(iii) 2(2x – 3) ≤ 6
(iv) – 4 < x < 4
(v) – 2 ≤ x < 5
(vi) 8 ≥ x > – 3
(vii) – 5 < x ≤ – 1
Solution:
(i) 2x – 1 < 5
2x < 5 + 1
2x < 6
x < 3
Representation on number line: –

(ii) 3x + 1 ≥ – 5
3x ≥-5 – 1
3x ≥ – 6
x ≥ – 2
Representation on number line:-

(iii) 2(2𝑥 − 3) ≤ 6
4𝑥 − 6 ≤ 6
4𝑥 ≤ 6 + 6
4𝑥 ≤ 12
𝑥 ≤ 3

(iv) – 4 < 𝑥 < 4 −4 < 𝑥 < 4

(v) −𝟐 ≤ 𝒙 < 𝟓 −𝟐 ≤ 𝒙 < 𝟓

(vi) 𝟖 ≥ 𝒙 > −𝟑
𝟖 ≥ 𝒙 > −𝟑

(vii) −𝟓 < 𝒙 ≤ −𝟏

Question 2. For each graph given, write an in-equation taking 𝒙 as the variable:

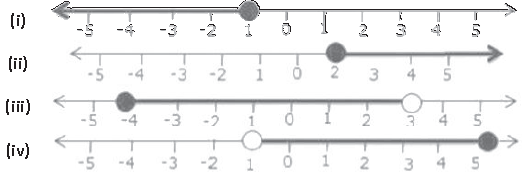
Solution :

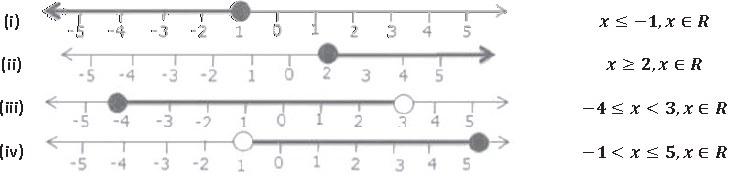
Question 3. For the following in-equations, graph the solution set on the real number line:
(i) −𝟒 ≤ 𝟑𝒙 − 𝟏 < 𝟖
(ii) 𝒙 − 𝟏 < 𝟑 − 𝒙 ≤ 𝟓
Solution :
(i) −4 ≤ 3𝑥 − 1 < 8
−4 ≤ 3𝑥 − 1 and 3𝑥 − 1 < 8
−4 + 1 ≤ 3𝑥 and 3𝑥 < 8 + 1
−3 ≤ 3𝑥 and 3𝑥 < 9
3𝑥 ≥ −3 and 3𝑥 < 9
𝑥 ≥ −1 and 𝑥 < 3

(ii) 𝑥 − 1 < 3 − 𝑥 ≤ 5
𝑥 − 1 < 3 − 𝑥 and 3 − 𝑥 ≤ 5
2𝑥 < 4 and − 𝑥 ≤ 5 − 3
𝑥 < 2 and 𝑥 ≤ −2

Question 4. Represent the solution of each of the following in-equalities on the real number line:
(i) 𝟒𝒙 − 𝟏 > 𝒙 + 𝟏𝟏
(ii) 𝟕 − 𝒙 ≤ 𝟐 − 𝟔𝒙
(iii) 𝒙 + 𝟑 ≤ 𝟐𝒙 + 𝟗
(iv) 𝟐 − 𝟑𝒙 > 𝟕 − 𝟓𝒙
(v) 𝟏 + 𝒙 ≥ 𝟓𝒙 − 𝟏𝟏
(vi) 𝟐𝒙 + 𝟓 / 𝟑 > 𝟑𝒙 − 𝟑
Solution:
(i) 4𝑥 − 1 > 𝑥 + 11
4𝑥 − 𝑥 > 11 + 1
3𝑥 > 12
𝑥 > 12 / 3
𝑥 > 4
Below is the representation on number line:-

(ii) 𝟕 − 𝒙 ≤ 𝟐 − 𝟔𝒙
− 𝑥 + 6𝑥 ≤ 2 − 7
5𝑥 ≤ −5
𝑥 ≤ − 5 / 5
𝑥 ≤ −1
Below is the representation on number line:-

(iii) 𝑥 + 3 ≤ 2𝑥 + 9
𝑥 − 2𝑥 ≤ 9 − 3
𝑥 − 2𝑥 ≤ 6
− 𝑥 ≤ 6
𝑥 ≥ −6
Below is the representation on number line:-

(iv) 2 − 3𝑥 > 7 − 5𝑥
−3𝑥 + 5𝑥 > 7 − 2
2𝑥 > 5
𝑥 > 2.5
Below is the representation on number line:-

(v) 1 + 𝑥 ≥ 5𝑥 − 11
1 + 11 ≥ 5𝑥 − 𝑥
12 ≥ 4𝑥
12 / 4 ≥ 𝑥
3 ≥ 𝑥
𝑥 ≤ 3
Below is the representation on number line:-

(vi) 2𝑥 + 5 / 3 > 3𝑥 − 3
2𝑥 + 5 > 3(3𝑥 − 3)
2𝑥 + 5 > 9𝑥 − 9
2𝑥 − 9𝑥 > −9 − 5
−7𝑥 > −14
𝑥 > 2
Below is the representation on number line:-

Question 5. 𝒙 ∈ {𝒓𝒆𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓𝒔} and −𝟏 < 𝟑 – 𝟐𝒙 ≤ 𝟕, evaluate 𝒙 and represent it on a number line.
Solution:
It is given that,
−1 < 3 – 2𝑥 ≤ 7
−1 < 3 – 2𝑥 and 3 – 2𝑥 ≤ 7
2𝑥 < 3 + 1 and – 2𝑥 ≤ 7 − 3
2𝑥 < 4 and − 2𝑥 ≤ 4
𝑥 < 2 and 𝑥 ≥ −2
Hence, the solution when 𝑥 ∈ 𝑅 is {-2 ≤ x < 2}.
Below is the representation on number line:-

Question 6. List the elements of the solution set of the in-equation. −𝟑 < 𝒙 – 𝟐 ≤ 𝟗 – 𝟐𝒙; 𝒙 ∈ 𝑵.
Solution:-
−3 < 𝑥– 2 ≤ 9 – 2𝑥
−3 < 𝑥– 2 and 𝑥– 2 ≤ 9– 2𝑥
−3 + 2 < 𝑥 and 𝑥 + 2𝑥 ≤ 9 + 2
−1 < 𝑥 and 3𝑥 ≤ 11
Hence, the solution when 𝑥 ∈ 𝑁 is {−1 < 𝑥 ≤ 11/3}.

Question 7. Find the range of values of 𝒙 which satisfies

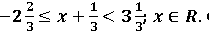
Graph these values of 𝒙 on the number line.
Solution :

Question 8. Find the value of x, which satisfy the in-equation:

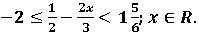
Graph these values of 𝒙 on the number line.
Solution :

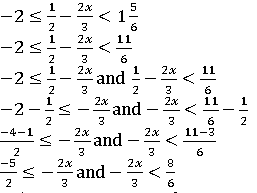
− 5 × 3 ≤ −2𝑥 × 2 and − 2𝑥 × 6 < 8 × 3
− 15 ≤ −4𝑥 and − 12𝑥 < 24
15/4 ≤ 𝑥 and 𝑥 < −2
3.75 ≥ 𝑥 and 𝑥 > −2
Hence, the solution is {1, 2, 3}.
Below is the representation on number line:-

Question 9. Given x ∈ {real numbers}, find the range of values of x for which -5 ≤ 2x – 3 < x + 2 and represent it on a number line.
Solution:
It is given that,
−5 ≤ 2𝑥– 3 < 𝑥 + 2
−5 ≤ 2𝑥– 3 and 2𝑥 – 3 < 𝑥 + 2
−2 ≤ 2𝑥 and 𝑥 < 5
−1 ≤ 𝑥 and 𝑥 < 5
Hence, the solution when 𝑥 ∈ 𝑅 is {−1 ≤ 𝑥 < 5}.
Below is the representation on number line:-

Question 10. If 5x – 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.
Solution :
It is given that,
5x – 3 ≤ 5 + 3x ≤ 4x + 2
5x – 3 ≤ 5 + 3x and 5 + 3x ≤ 4x + 2
5x – 3x ≤ 5 + 3 and 3x – 4x ≤ 2 – 5
2x ≤ 8 and – x ≤ – 3
x ≤ 8/2 and – x ≤ – 3
x ≤ 4 and x ≥ 3
3 ≤ x ≤ 4
a = 3 and b = 4.
Hence, the value of a and b is 3 and 4 respectively.

Question 11. Solve the following in – equation and graph the solution set on the number line:
2x – 3 < x + 2 ≤ 3x + 5,x ∈ R.
Solution :
It is given that,
2x – 3 < x + 2 ≤ 3x + 5
2x – 3 < x + 2 and x + 2 ≤ 3x + 5
2x – x < 2 + 3 and 2 – 5 ≤ 3x – x
x < 5 and – 3 ≤ 2x
x < 5 and – 1.5 ≤ x
Hence, the solution { – 1.5 ≤ x < 5}.

Question 12. Solve and graph the solution set of:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25,x ∈ R
(ii) 2x – 9 ≤ 7 and 3x + 9 > 25,x ∈ I
(iii) x + 5 ≥ 4(x – 1) and 3 – 2x < – 7,x ∈ R
Solution:
(i) It is given that,
2x – 9 < 7 and 3x + 9 ≤ 25
2x < 7 + 9 and 3x ≤ 25 – 9
2x < 16 and 3x ≤ 16

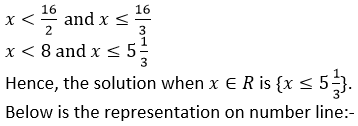
(iii) It is given that,
x + 5 ≥ 4(x – 1) and 3 – 2x < – 7,x ∈ R
x + 5 ≥ 4x – 4 and 3 – 2x < – 7
x – 4x ≥ – 4 -5 and – 2x < – 7-3
-3x ≥ – 9 and – 2x < – 10
x ≤ 3 and x > 5

Question 13. Solve and graph the solution set of:
(i) 3x – 2 > 19 or 3 – 2x ≥ – 7,x ∈ R
(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1 ≤ 17,p ∈ R
Solution:
(i) It is given that,
3x – 2 > 19 or 3 – 2x ≥ – 7
3x – 2 > 19 or 3 – 2x ≥ – 7
3x > 21 or – 2x ≥ – 10
x > 7 or x ≤ 5
Hence, the solution set is x > 7 or x ≤ 5.
Below is the representation on number line: –

(ii) It is given that,
5 > p –1 > 2 or 7 ≤ 2p–1 ≤ 17
5 + 1 > p > 2 + 1 or 7 + 1 ≤ 2p ≤ 17 + 1
6 > p > 3 or 8 ≤ 2p ≤ 18
6 > p > 3 or 4 ≤ p ≤ 9
Hence, the solution set is 6 > p > 3 or 4 ≤ p ≤ 9.
Below is the representation on number line:-

Question 14. The diagram represents two in-equations A and B on real number lines:

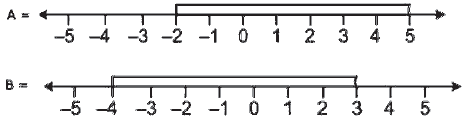
(i) Write down A and B in set builder notation.
(ii) Represent 𝐀 ∪ 𝐁 and 𝐀 ∩ 𝐁′ on two different number lines.
Solution:
(i) By the line diagram:
A = {𝑥 ∈ 𝑅: −2 ≤ 𝑥 < 5}
B = {𝑥 ∈ 𝑅: −4 ≤ 𝑥 < 3}
(ii) Here A = {𝑥 ∈ 𝑅: −2 ≤ 𝑥 < 5} and B = {𝑥 ∈ 𝑅: −4 ≤ 𝑥 < 3}
A ∩ B = {𝑥 ∈ 𝑅: −2 ≤ 𝑥 < 5}
Below is the representation on number line:-

B’ = {𝑥 ∈ 𝑅: 3 < 𝑥 ≤ −4}
A ∩ B’ = {𝑥 ∈ 𝑅: 3 ≤ 𝑥 < 5}
Below is the representation on number line:-

Question 15. Use real number line to find the range of values of x for which:
(i) x > 3 and 0 < x < 6
(ii) x < 0 and – 3 ≤ x < 1
(iii) – 1 < x ≤ 6 and – 2 ≤ x ≤ 3 
Solution:
(i) x > 3 and 0 < x < 6
In the range where their graphs on the real number lines meet, both in – equations are true.
Below is the representation on number line: –

The common range of the graph is 3 < x < 6.

(ii) x < 0 and – 3 ≤ x < 1
In the range where their graphs on the real number lines meet, both in – equations are true.
Below is the representation on number line: –

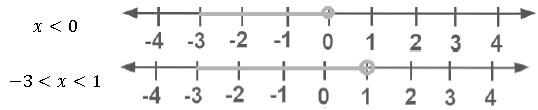
The common range of the graph is – 3 ≤ x < 1.

(iii) – 1 < x ≤ 6 and – 2 ≤ x ≤ 3
In the range where their graphs on the real number lines meet, both in – equations are true.
Below is the representation on number line: –

The common range of the graph is – 1 < x ≤ 3.

Question 16. Illustrate the set {x: – 3 ≤ x < 0 or x > 2,x ∈ R} on the real number line.
Solution:
It is given that,
– 3 ≤ x < 0 or x > 2
Graph of points which belong to – 3 ≤ x < 0 or x > 2 or both.
Below is the representation on number line: –

Question 17. Given A = {x: – 1 < x ≤ 5,x ∈ R} and B = {x: – 4 ≤ x < 3,x ∈ R} Represent on different number lines:
(i) A∩B
(ii) A’∩B
(iii) A –B
Solution:
It is given that,
A = {x: – 1 < x ≤ 5,x ∈ R}
B = {x: – 4 ≤ x < 3,x ∈ R}

(i) A∩B
{x: – 1 < x ≤ 3,x ∈ R}
Below is the representation on number line: –

(iii) A –B
{x: 3 ≤ x ≤ 5, x ∈ R}
Below is the representation on number line:-

Question 18. P is the solution set of 7x–2 > 4x + 1 and Q is the solution set of 9x–45 ≥ 5(x – 5); where x ∈ R. Represent:
(i) P∩Q
(ii) P – Q
(iii) P∩Q’
On different number lines.
Solution:
It is given that,
P = {x:7x – 2 > 4x + 1,x ∈ R}
7x – 2 > 4x + 1
7x – 4x > 1 + 2
3x > 3
x > 1
Q = {x:9x – 45 ≥ 5(x – 5),x ∈ R}
9x – 45 ≥ 5x – 25
9x – 5x ≥ – 25 + 45
4x ≥ 20
x ≥ 5
(i) P∩Q
{x:x ≥ 5,x ∈ R}
Below is the representation on number line: –

(ii) P – Q
{x:1 < x < 5,x ∈ R}
Below is the representation on number line: –

(iii) P∩Q’
{x:1 < x < 5,x ∈ R}
Below is the representation on number line: –

Question 19. Find the range of value of x, which satisfy:

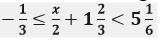
Graph, in each of the following cases, the values of x on the different real number lines:
(i) x ∈ W
(ii) x ∈ Z
(iii) x ∈ R
Solution :
It is given that,

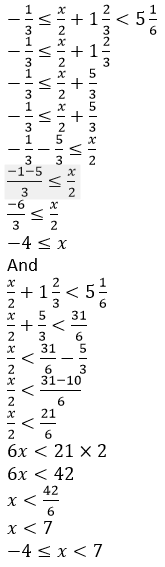
(i) x ∈ W
The range of the value of x is {0, 1, 2, 3, 4, 5}
Below is the representation on number line:-

(ii) x∈Z
The range of the value of x is {0, 1, 2, 3, 4, 5,}
Below is the representation on number line: –

(iii) x ∈ R
The range of value of x is – 4 ≤ x ≤ 7.
Below is the representation on number line: –

Question 20. Given: A = {x: – 8 < 5x + 2 ≤ 17,x ∈ I}, B = {x: – 2 ≤ 7 + 3x < 17,x ∈ R}
Where R = {real numbers} and I = {integers}. Represent A and B on two different number lines. Write down the elements of A ∩ B.
Solution :
It is given that,
A = {x: – 8 < 5x + 2 ≤ 17,x ∈ I}
– 8 < 5x + 2 ≤ 17
– 8 < 5x + 2 and 5x + 2 ≤ 17
– 8 – 2 < 5x and 5x ≤ 17 – 2
– 10 < 5x and 5x ≤ 15
– 2 < x and x ≤ 3
Hence, the solution is – 2 < x ≤ 3 x ∈ I

B = {x: – 2 ≤ 7 + 3x < 17,x ∈ R}
– 2 ≤ 7 + 3x and 7 + 3x < 17
– 3x ≤ 7 + 2 and 3x < 17 – 7
– 3x ≤ 9 and 3x < 10
x ≤ – 3 and x < 3.33
Hence, the solution is – 3 ≤ x < 3.33,x ∈ R
A∩B={ – 1,0,1,2,3}

Question 21. Solve the following in – equation and represent the solution set on the number line 2x –5 ≤ 5x + 4 < 11, where x ∈ I
Solution :
It is given that,
2x – 5 ≤ 5x + 4 < 11
2x – 5 ≤ 5x + 4 and 5x + 4 < 11
2x – 5x ≤ 4 + 5 and 5x < 11 – 4
– 3x ≤ 9 and 5x < 7
– 3x ≤ 9 and 5x < 7
x ≤ – 9/3 and x < 7/5
x ≤ – 3 and x < 1.4
– 3 ≥ x < 1.4
Hence, the solution set is { – 3, – 2, – 1,0,1}
Below is the representation on number line: –

Question 22. Given that 𝒙 ∈ 𝑰, solve the in-equation and graph the solution on the number line:

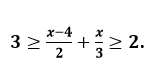
Solution :
It is given that,

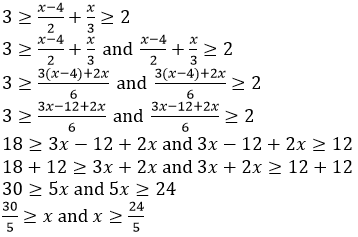
6 ≥ x and x ≥ 4.8
6 ≥ x ≥ 4.8
Hence, the solution set is {5,6
Below is the representation on number line:-

Question 23. Given:
A = {x: 11x – 5 >7x + 3,x ∈ R} and B = {x: 18x – 9 ≥15+12x, x ∈ R}. Find the range of set A∩B and represent it on number line.
Solution:
It is given that,
A = {𝑥: 11𝑥– 5 > 7𝑥 + 3, 𝑥 ∈ 𝑅}
11𝑥– 7𝑥 > 3 + 5
4𝑥 > 8
𝑥 > 8/4
𝑥 > 2
Hence, the solution set {𝑥: 𝑥 > 2, 𝑥 ∈ 𝑅}
B = {𝑥: 18𝑥 – 9 ≥ 15 + 12𝑥, 𝑥 ∈ 𝑅}
18𝑥 – 12𝑥 ≥ 15 − 9
6𝑥 ≥ 24
𝑥 ≥ 24/6
𝑥 ≥ 4
Hence, the solution set is {𝑥: 𝑥 ≥ 4, 𝑥 ∈ 𝑅}
𝐴 ∩ 𝐵 = {𝑥: 𝑥 ≥ 4, 𝑥 ∈ 𝑅}
Below is the representation on number line:-

Question 24. Find the set of values of x satisfying

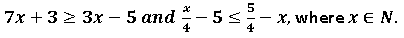
Solution :
It is given that,
7𝑥 + 3 ≥ 3𝑥 − 5
7𝑥 − 3𝑥 ≥ −5 − 3
4𝑥 ≥ −8
𝑥 ≥ −2
And

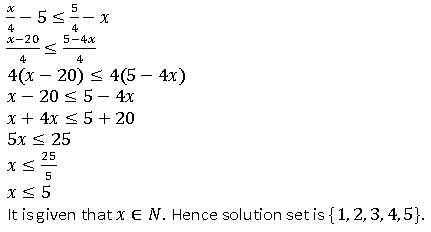
Question 25. Solve:

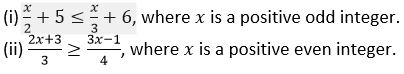
It is given that as x is a positive even integer. Hence the solution set is {2, 4, 6, 8, 10, 12, 14}.

Question 26. Solve the in-equation:

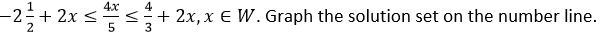
Question 27. Find three consecutive largest positive integers such that the sum of one-third of first, one fourth
of second and one-fifth of third is at most 20.
Solution :
Let the first integer will be 𝑥
Second integer will be 𝑥 + 1
Third integer will be 𝑥 + 2
It is given that,

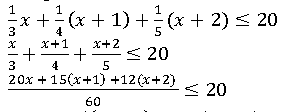
20𝑥 + 15(𝑥 + 1) + 12(𝑥 + 2) ≤ 20 × 60
20𝑥 + 15𝑥 + 15 + 12𝑥 + 24 ≤ 1200
20𝑥 + 15𝑥 + 12𝑥 ≤ 1200 − 15 − 24
47𝑥 ≤ 1161
x ≤ 1161/47
x ≤ 24.702
The first positive integer will be 24
Second integer be 24 + 1 = 25
Third integer be 24 + 2 = 26
Hence, the required integers are 24, 25 and 26.

Question 28. Solve the given inequation and graph the solution on the number line
𝟐𝒚– 𝟑 < 𝒚 + 𝟏 ≤ 𝟒𝒚 + 𝟕, 𝒚 ∈ 𝑹
Solution:
It is given that,
2𝑦 – 3 < 𝑦 + 1 ≤ 4𝑦 + 7, 𝑦 ∈ 𝑅
2𝑦– 3 < 𝑦 + 1 𝑎𝑛𝑑 𝑦 + 1 ≤ 4𝑦 + 7
2𝑦 – 𝑦 < 1 + 3 𝑎𝑛𝑑 𝑦 − 4𝑦 ≤ 7 − 1
𝑦 < 4 𝑎𝑛𝑑 − 3𝑦 ≤ 6
𝑦 < 4 𝑎𝑛𝑑 𝑦 ≤ − 6/3
𝑦 < 4 𝑎𝑛𝑑 𝑦 ≤ −2
– 2 ≤ 𝑦 < 4
Hence, the solution set is {– 2 ≤ 𝑦 < 4, 𝑦 ∈ 𝑅}

Question 29. Solve the in-equation: 𝟑𝒛– 𝟓 ≤ 𝒛 + 𝟑 < 𝟓𝒛 – 𝟗, 𝒛 ∈ 𝑹. Graph the solution set on the number line.
Solution :
It is given that,
3𝑧– 5 ≤ 𝑧 + 3 < 5𝑧 – 9, 𝑧 ∈ 𝑅
3𝑧– 5 ≤ 𝑧 + 3 and 𝑧 + 3 < 5𝑧 – 9
3𝑧– 𝑧 ≤ 3 + 5 and 𝑧 − 5𝑧 < – 9 − 3
2𝑧 ≤ 8 and − 4𝑧 < – 12
z ≤ 8/2 and 𝑧 < –12/−4
z ≤ 4 and 𝑧 < 3
Below is the representation on number line:-

Question 30. Solve the following inequation and represent the solution set on the number line.

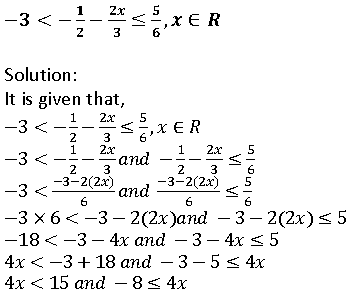
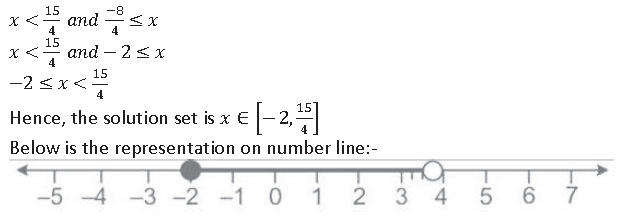
Question 31. Solve the following inequation and represent the solution set on the number line:

Question 32. Solve the following in equation, write the solution set and represent it on the number line:

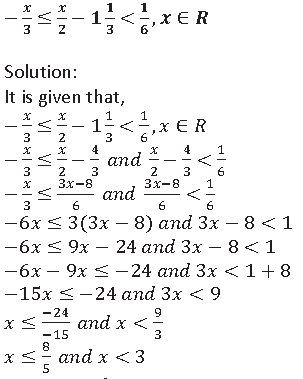
𝑥 ≤ 1.6 𝑎𝑛𝑑 𝑥 < 3
1.6 ≤ 𝑥 < 3
Hence, the solution set is {1.6 ≤ 𝑥 < 3}
Below is the representation on number line:-

Question 33. Find the values of 𝒙, which satisfy the inequation −𝟐 𝟓/𝟔 < 𝟏/𝟐 −(𝟐𝒙/𝟑) ≤ 𝟐, 𝒙 ∈ 𝑾. Graph the solution set on the number line.
Solution:
It is given that,

Question 34. Solve the following in equation and write the solution set: 𝟏𝟑𝒙– 𝟓 < 𝟏𝟓𝒙 + 𝟒 < 𝟕𝒙 + 𝟏𝟐, 𝒙 ∈ 𝑹 Solution :
It is given that,
13𝑥– 5 < 15𝑥 + 4 < 7𝑥 + 12, 𝑥 ∈ 𝑅
13𝑥– 5 < 15𝑥 + 4 𝑎𝑛𝑑 15𝑥 + 4 < 7𝑥 + 12
13𝑥– 15𝑥 < 4 + 5 𝑎𝑛𝑑 15𝑥 − 7𝑥 < 12 − 4
−2𝑥 < 9 𝑎𝑛𝑑 8𝑥 < 8
𝑥 > − 9/2 𝑎𝑛𝑑 𝑥 < 8/8
𝑥 > −4.5 𝑎𝑛𝑑 𝑥 < 1
−4.5 < 𝑥 < 1
Hence, the solution set is {−4.5 < 𝑥 < 1}.
Below is the representation on number line:-

Question 35. Solve the following inequation, write the solution set and represent it on the number line.
−𝟑(𝒙 – 𝟕) ≥ 𝟏𝟓 – 𝟕𝒙 > 𝒙 + 𝟏/𝟑 , 𝒙 ∈ 𝑹.
Solution:
It is given that,

Question 36. Solve the following inequation and represent the solution set on a number line.