Selina ICSE Class 10 Maths Solutions Chapter 7 Ratio And Proportion Including Properties Uses

Question 1. If a:b = 5:3, find:

Question 2. If x: y = 4: 7, find the value of (3𝑥 + 2𝑦): (5𝑥 + 𝑦).
Solution:
It is given that,
𝑥: 𝑦 = 4: 7
𝑥/𝑦 = 4/7
Divide each term by 𝑦.

Question 3. If a:b = 3:8,

Question 4. If (a – b): (a + b) = 1: 11, find the ratio (5a + 4b + 15): (5a – 4b + 3).
Solution:
It is given that,

Question 5. Find the number which bears the same ratio to 7/33 that 8/21 does to 4/9.
Solution:
Let us assumed that,
The required fraction be 𝑥/𝑦

Question 7. Find 𝑥/𝑦, when 𝑥² + 6𝑦² = 5𝑥𝑦
Solution:
It is given that,
𝑥² + 6𝑦² = 5𝑥𝑦
By dividing both the sides by 𝑦²

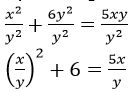
Let us assumed that, 𝑥/𝑦 = 𝑎
𝑎² + 6 = 5𝑎
𝑎² − 5𝑎 + 6 = 0
𝑎² − 2𝑎 − 3𝑎 + 6 = 0
𝑎(𝑎 − 2) − 3(𝑎 − 2) = 0
(𝑎 − 3)(𝑎 − 2) = 0
𝑎 − 3 = 0          𝑎 − 2 = 0
𝑎 = 3                𝑎 = 2
Hence, the value of 𝑥/𝑦 is 2 and 3.

Question 8. If the ratio between 8 and 11 is the same as the ratio of 2𝑥 − 𝑦 to 𝑥 + 2𝑦, find the value of 7𝑥/9𝑦.
Solution:
It is given that,

Question 9. Divide Rs. 1290 into A, B and C such that A is 2/5 of B and B:C = 4:3.
Solution:
It is given that,

Question 10. A school has 630 students. The ratio of the number of boys to the number of girls is 3 : 2. This ratio changes to 7 : 5 after the admission of 90 new students. Find the number of newly admitted boys.
Solution:
Let us assumed that,
Number of boys are 3𝑥
and number of girls are 2𝑥
3𝑥 + 2𝑥 = 630
5𝑥 = 630
𝑥 = 630/5
𝑥 = 126
Number of boys = 3 × 126 = 378
Number of girls = 2 × 126 = 252
According to question,
Admission of 90 new students,
Total number of students = 630 + 90
Total number of students = 720
Let us assumed that,
Number of boys are 7𝑥
and number of girls are 5𝑥
7𝑥 + 5𝑥 = 720
12𝑥 = 720
𝑥 = 720/12
𝑥 = 60
Number of boys = 7 × 60 = 420
Number of girls = 5 × 60 = 300
Hence, the number of new students boys are 420– 378 = 42.

Question 11. What quantity must be subtracted from each term of the ratio 9: 17 to make it equal to 1: 3
Solution:
Let us assumed that,
𝑥 be deducted from each term of the 9:17 ratio.
9−𝑥/17− 𝑥 = 1/3
By cross-multiplication,
3(9 − 𝑥) = 17 − 𝑥
27 − 3𝑥 = 17 − 𝑥
−3𝑥 + 𝑥 = 17 − 27
−2𝑥 = −10
𝑥 = 10/2
𝑥 = 5
Hence, subtract the required number from the total 5.

Question 12. The monthly pocket money of Ravi and Sanjeev are in the ratio 5 : 7. Their expenditures are in the ratio 3 : 5. If each saves Rs. 80 every month, find their monthly pocket money.
Solution:
It is given that,
The pocket money of Ravi and Sanjeev are in the Ratio 5:7
The pocket expenditures of Ravi and Sanjeev are in the Ratio 3:5
And each of them saves Rs. 80.
Let us assumed that,
Pocket money of Ravi and Sanjeev are in the Ratio 5k and 7k
Pocket expenditures of Ravi and Sanjeev are in the Ratio 3m and 5m
5𝑘 − 3𝑚 = 80___________(i)
7𝑘 − 5𝑚 = 80___________(ii)
From equation (i) we get the value of k
5𝑘 − 3𝑚 = 80

Question 13. The work done by (𝑥– 2) men in (4𝑥 + 1) days and the work done by (4𝑥 + 1) men in (2𝑥– 3) days are in the ratio 3: 8. Find the value of 𝑥.
Solution:
It is given that,
Number of men = (𝑥– 2)
Number of days = (4𝑥 + 1)
Amount of work done by = (𝑥– 2)(4𝑥 + 1)units of work
Similarly,
Number of men = (4𝑥 + 1)
Number of days = (2𝑥 − 3)
Amount of work done by = (4𝑥 + 1)(2𝑥 – 3)units of work
According to question,

By Cross-multiply,
8(𝑥 − 2) = 3(2𝑥 − 3)
8𝑥 − 16 = 6𝑥 − 9
8𝑥 − 6𝑥 = −9 + 16
2𝑥 = 7
𝑥 = 7/2
𝑥 = 3.5
Hence, the value of 𝑥 is 3.5.

Question 14. The bus fare between two cities is increased in the ratio 7: 9. Find the increase in the fare, if:
(i) the original fare is Rs 245;
(ii) the increased fare is Rs 207.
Solution:
It is given that,
Bus fare between two cities is increased in the ratio 7:9.
New bus fare = 9/7 × Original bus fare
(i) New bus fare = 9/7 × 245
New bus fare = Rs. 315
Increase in fare = Rs. 315 – Rs. 245
Increase in fare = Rs. 70
(ii) Rs. 207 = 9/7 × Original bus fare
Rs. 207 × 7/9 = Original bus fare
Original bus fare = Rs. 161
Increase in fare = Rs. 207 – Rs. 161
Increase in fare = Rs. 46

Question 15. By increasing the cost of entry ticket to a fair in the ratio 10: 13, the number of visitors to the fair has decreased in the ratio 6: 5. In what ratio has the total collection increased or decreased?
Solution:
Let us assumed that,
The initial cost of the entry ticket is 10𝑥 and present cost be 13𝑥.
The initial number of the visitors are 6𝑦 and at present number of visitor be 5𝑦.
Total collection = 10𝑥 × 6𝑦 = 60𝑥𝑦
Total collection = 13𝑥 × 5𝑦 = 65𝑥𝑦
Ratio of total collection = 60𝑥𝑦 ∶ 65𝑥𝑦 = 12 ∶ 13
Hence, the total collection has increased in the ratio 12: 13.

Question 16. In a basket, the ratio between the number of oranges and the number of apples is 7: 13. If 8 oranges and 11 apples are eaten, the ratio between the number of oranges and the number of apples
becomes 1: 2. Find the original number of oranges and the original number of apples in the basket.
Solution:
Let us assumed that,
The original number of oranges and apples be 7𝑥 and 13𝑥.
According to the question,
7𝑥− 8/13𝑥 −11 = 1/2
By cross-multiplication,
2(7𝑥 − 8) = 13𝑥 − 11
14𝑥 − 16 = 13𝑥 − 11
14𝑥 − 13𝑥 = −11 + 16
𝑥 = 5
Hence, the original number of oranges is 35 and apples are 65 respectively.

Question 17. In a mixture of 126 kg of milk and water, milk and water are in ratio 5 : 2. How much water must be added to the mixture to make this ratio 3 : 2?
Solution:
It is given that,
The ratio of quantity of milk and water is 5:2
Total mixture is 126 kg
Quantity of milk = 126 × 5/7
Quantity of milk = 90kg.
Quantity of milk = 126 × 2/7
Quantity of milk = 36kg.
Change Ratio of mixture is 3:2
Let the quantity of water be added be 𝑥kg

Question 18. (A) If A: B = 3: 4 and B: C = 6: 7, find:
(i) A: B: C
(ii) A: C
(B) If A : B = 2 : 5 and A : C = 3 : 4, find:
(i) A : B : C
Solution:
(A) A: B = 3: 4 and B: C = 6: 7
(i) A: B: C
It is given that,

Question 19 (i). If 3A = 4B = 6C; find A: B: C.
Solution:
It is given that,
3𝐴 = 4𝐵 = 6𝐶
From 3𝐴 = 4𝐵 we get,

Question 19 (ii). If 2a = 3b and 4b = 5c, find: a : c.
Solution:
It is given that,
2a = 3b and 4b = 5c
2a = 3b

Question 20. Find the compound ratio of:
(𝑖)3: 5 𝑎𝑛𝑑 8: 15
(𝑖𝑖) 2: 3, 9: 14 𝑎𝑛𝑑 14: 27
(𝑖𝑖𝑖) 2𝑎: 3𝑏, 𝑚𝑛: 𝑥2 𝑎𝑛𝑑 𝑥: 𝑛
(iv) √2: 1, 3: √5 𝑎𝑛𝑑 √20: 9
Solution:
(𝑖) 3: 5 𝑎𝑛𝑑 8: 15
It is given that,
3: 5 𝑎𝑛𝑑 8: 15
Compound ratio = 3 × 8: 5 × 15

Question 21. Find duplicate ratio of:
(𝑖) 3: 4 (𝑖𝑖) 3√3 ∶ 2√5
Solution:
(i) Duplicate ratio of 3: 4
= 3 × 2: 4 × 2
= 9: 16
Hence, the duplicate ratio is 9: 16
(ii) Duplicate ratio of 3√3: 2√5
= (3√3)2: (2√5)²
= 3√3 × 3√3: 2√5 × 2√5
= 9 × 3: 4 × 5
= 27: 20
Hence, the duplicate ratio is 27: 20

Question 22. Find the triplicated of:
(i) 1: 3 (ii) 𝑚/2 : 𝑛/3
Solution:
(i) Triplicated ratio of 1: 3
= (1)³: (3)³
= 1: 27
Hence, the triplicated ratio is 1: 27.

Question 23. Find sub-duplicate ratio of:
(i) 9: 16
(ii) (𝑥– 𝑦)⁴: (𝑥 + 𝑦)⁶
Solution:
(i) 9: 16
Sub-duplicate ratio of 9: 16
= √9: √16
= 3: 4
Hence, the sub-duplicate ratio is 3:4.
(ii) (𝑥– 𝑦)⁴: (𝑥 + 𝑦)⁶
Sub-duplicate ratio of 9: 16

Question 24. Find the sub-triplicate ratio of:
(i) 64: 27
(ii) 𝑥³: 125𝑦³
Solution:
(i) 64: 27
Sub-triplicate ratio of 64 : 27
= √64 3
: √27 3
= 4: 3
Hence, the sub-triplicate ratio is 4: 3.
(ii) 𝑥³: 125𝑦³
Sub-triplicate ratio of 𝑥³: 125𝑦³
= 3√𝑥³: 3√(5𝑦)³
= 𝑥: 5𝑦
Hence, the sub-triplicate ratio is 𝑥: 5𝑦.

Question 25. Find the reciprocal ratio of:
(i) 5:8
(ii) 𝑥/3 : 𝑦/7
Solution:

Question 26. If (𝑥 + 3): (4𝑥 + 1) is the duplicate ratio of 3: 5, find the value of 𝑥.
Solution:
It is given that,
(𝑥 + 3): (4𝑥 + 1)
The duplicate Ratio = 3: 5

Question 27. If 𝑚: 𝑛 is the duplicate ratio of 𝑚 + 𝑥: 𝑛 + 𝑥; show that 𝑥² = mn.
Solution:
It is given that,

By cross-multiplication
𝑚(𝑛² + 2𝑛𝑥 + 𝑥²) = 𝑛(𝑚² + 2𝑚𝑥 + 𝑥²)
𝑚𝑛² + 2𝑚𝑛𝑥 + 𝑚𝑥² = 𝑛𝑚² + 2𝑚𝑛𝑥 + 𝑛𝑥²
𝑚𝑛² + 𝑚𝑥² = 𝑛𝑚² + 𝑛𝑥²
𝑚𝑛² − 𝑛𝑚² = 𝑛𝑥² − 𝑚𝑥²
𝑚𝑛(𝑛 − 𝑚) = 𝑥²(𝑛 − 𝑚)
𝑚𝑛 = 𝑥²
𝑥² = 𝑚𝑛
Hence proved

Question 28. If (3𝑥– 9): (5𝑥 + 4) is the triplicate ratio of 3: 4, find the value of 𝑥.
Solution:
It is given that,
(3𝑥– 9): (5𝑥 + 4)
Triplicate Ratio = 3: 4

By cross-multiplication,
64(𝑥 − 3) = 9(5𝑥 + 4)
64𝑥 − 192 = 45𝑥 + 36
64𝑥 − 45𝑥 = 192 + 36
19𝑥 = 228
𝑥 = 228/19
𝑥 = 12
Hence, the value of 𝑥 is 12.

Question 29. Find the ratio compounded of the reciprocal ratio of 15: 28, the sub-duplicate ratio of 36: 49 and the triplicate ratio of 5: 4.
Solution:
Reciprocal ratio of 15: 28
= 28: 15
Sub-duplicate ratio of 36: 49
= √36: √49
= 6: 7
Triplicate ratio of 5: 4
= 5³: 4³
= 125: 64

Question 30 (a). If 𝑟² = 𝑝𝑞, show that 𝑝: 𝑞 is the duplicate ratio of (𝑝 + 𝑟): (𝑞 + 𝑟).
Solution:
It is given that,
𝑟² = 𝑝𝑞
Duplicate ratio of (𝑝 + 𝑟): (𝑞 + 𝑟) = (𝑝 + 𝑟)²: (𝑞 + 𝑟)²
We know that,
(𝑎 + 𝑏)² = 𝑎² + 2𝑎𝑏 + 𝑏²
= (𝑝² + 2𝑝𝑟 + 𝑟²): (𝑞² + 2𝑞𝑟 + 𝑟²)
Put the value of 𝑟²
= (𝑝² + 2𝑝𝑟 + 𝑝𝑞): (𝑞² + 2𝑞𝑟 + 𝑝𝑞)
= 𝑝(𝑝 + 2𝑟 + 𝑞): 𝑞(𝑞 + 2𝑟 + 𝑝)

Question 30 (b). If (𝑝 − 𝑥): (𝑞 − 𝑥) be the duplicate ratio of 𝑝: 𝑞 then show that: 1/𝑝 + 1/𝑞 = 1/𝑥
Solution:
It is given that,

Exercise 7 B

Question 1. Find the fourth proportional to:
(i) 1.5, 4.5 𝑎𝑛𝑑 3.5
(ii) 3𝑎, 6𝑎² 𝑎𝑛𝑑 2𝑎𝑏²
Solution:
(i) Let us assumed that,
The fourth proportional to 1.5, 4.5 and 3.5 be 𝑥.
1.5: 4.5 = 3.5: 𝑥
1.5 × 𝑥 = 3.5 × 4.5
1.5 × 𝑥 = 15.75
𝑥 = 10.5
Hence, the fourth proportional to 1.5, 4.5 and 3.5 is 10.5.
(ii) Let us assumed that,
The fourth proportional to 3𝑎, 6𝑎² and 2𝑎𝑏² be 𝑥.
3𝑎: 6𝑎² = 2𝑎𝑏²: 𝑥
3𝑎 × 𝑥 = 2𝑎𝑏² × 6𝑎²
3𝑎 × 𝑥 = 12𝑎3𝑏²
𝑥 = 12𝑎³𝑏²/3𝑎
𝑥 = 4𝑏²𝑏²
Hence, the fourth proportional to 3𝑎, 6𝑎² and 2𝑎𝑏² is 4𝑎2𝑏².

Question 2. Find the third proportional to:
(𝑖) 2 (2/3) 𝑎𝑛𝑑 4
(𝑖𝑖) 𝑎 − 𝑏 𝑎𝑛𝑑 𝑎² − 𝑏²
Solution:
(i) Let us assumed that,
The third proportional to 2 (2/3) 𝑎𝑛𝑑 4 be 𝑥
We know that,
Given ratios are in continue proportion

(ii) Let us assumed that,
The third proportional to 𝑎 − 𝑏 𝑎𝑛𝑑 𝑎² − 𝑏² be 𝑥
We know that,
Given ratios are in continue proportion
𝑎 − 𝑏: 𝑎² − 𝑏² = 𝑎² − 𝑏²: 𝑥

Question 3. Find the mean proportional between:
(i) 6 + 3√3 𝑎𝑛𝑑 8 − 4√3
(ii) 𝑎 − 𝑏 𝑎𝑛𝑑 𝑎³ − 𝑎²𝑏
Solution:
(i) Let us assumed that,
The mean proportional between 6 + 3√3 𝑎𝑛𝑑 8 − 4√3 be 𝑥.
6 + 3√3, 𝑥 𝑎𝑛𝑑 8– 4√3
6 + 3√3 ∶ 𝑥 = 𝑥 ∶ 8 – 4√3
𝑥 × 𝑥 = (6 + 3√3)(8– 4√3)
𝑥² = 48 + 24√3 − 24√3– 36
𝑥² = 12
𝑥 = 2√3
Hence, the mean proportional between 6 + 3√3 𝑎𝑛𝑑 8 − 4√3 is 2√3.
(ii) Let us assumed that,
The mean proportional between 𝑎– 𝑏 𝑎𝑛𝑑 𝑎³– 𝑎²𝑏 be 𝑥.
𝑎– 𝑏, 𝑥 𝑎𝑛𝑑 𝑎³– 𝑎²𝑏
𝑎 – 𝑏: 𝑥 = 𝑥: 𝑎³– 𝑎²𝑏
𝑥 × 𝑥 = (𝑎 – 𝑏) (𝑎³– 𝑎²𝑏)
𝑥² = (𝑎 – 𝑏)𝑎²(𝑎 – 𝑏)
𝑥 = [𝑎(𝑎– 𝑏)]
𝑥 = 𝑎(𝑎 – 𝑏)
Hence, the mean proportional between 𝑎 − 𝑏 𝑎𝑛𝑑 𝑎³ − 𝑎²𝑏 is 𝑎(𝑎 – 𝑏)

Question 4. If 𝑥 + 5 is the mean proportional between 𝑥 + 2 and 𝑥 + 9; find the value of 𝑥.
Solution:
It is given that,
𝑥 + 5 is the mean proportional between 𝑥 + 2 and 𝑥 + 9.
(𝑥 + 2), (𝑥 + 5) and (𝑥 + 9)
(𝑥 + 2): (𝑥 + 5) = (𝑥 + 5): (𝑥 + 9)

By cross multiply,
(𝑥 + 2)(𝑥 + 9) = (𝑥 + 5)²
𝑥² + 2𝑥 + 9𝑥 + 18 = 𝑥² + 25 + 10𝑥
11𝑥 − 10𝑥 = 25 − 18
𝑥 = 7
Hence, the value of 𝑥 is 7.

Question 5. If 𝑥², 4 and 9 are in continued proportion, find x.
Solution:
It is given that,
𝑥², 4 and 9 are in continued proportion
𝑥²: 4 = 4: 9

Question 6. What least number must be added to each of the numbers 6, 15, 20 and 43 to make them proportional?
Solution:
Let us assumed that,
The number added be 𝑥.
(6 + 𝑥): (15: 𝑥): : (20 + 𝑥): (43 + 𝑥)

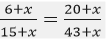
By cross multiply
(6 + 𝑥)(43 + 𝑥) = (20 + 𝑥)(15 + 𝑥)
258 + 6𝑥 + 43𝑥 + 𝑥² = 300 + 20𝑥 + 15𝑥 + 𝑥²
258 + 49𝑥 = 300 + 35𝑥
49𝑥 − 35𝑥 = 300 − 258
14𝑥 = 42
𝑥 = 42/14
𝑥 = 3
Hence, the value of 𝑥 is 3.

Question 7 (i). If a, b, c are in continued proportion.

Question 7 (ii). If 𝑎, 𝑏, 𝑐 are in continued proportion and 𝑎(𝑏 − 𝑐) = 2𝑏. Prove that: 𝑎 − 𝑐 = 2(𝑎+𝑏)/𝑎
Solution:
It is given that,
a, b and c are in continued proportion,
𝑎/𝑏 = 𝑏/𝑐
By cross multiplication,
𝑎𝑐 = 𝑏²
Put the value of ac in given equation,
𝑎(𝑏 − 𝑐) = 2𝑏
𝑎𝑏 − 𝑎𝑐 = 2𝑏
𝑎𝑏 − 𝑏² = 2𝑏
𝑏(𝑎 − 𝑏) = 2𝑏
𝑎 − 𝑏 = 2
Now,
In the LHS side it is given that,

Question 8. What least number must be subtracted from each of the numbers 7, 17 and 47 so that the remainders are in continued proportion?
Solution:
It is given that,
7, 17 and 47 so that the remainders are in continued proportion
Let us assumed that,
The subtracted number be 𝑥
(7 − 𝑥): (17 − 𝑥): : (17 − 𝑥): (47 − 𝑥)

By cross multiplication,
(7 − 𝑥)(47 − 𝑥) = (17 − 𝑥)(17 − 𝑥)
329 − 47𝑥 − 7𝑥 + 𝑥² = 289 − 34𝑥 + 𝑥2
329 − 54𝑥 = 289 − 34𝑥
329 − 54𝑥 + 34𝑥 = 289 − 329
−20𝑥 = −40
𝑥 = 40/20
𝑥 = 2
Hence, the number which should be subtracted is 2.

Question 9. If y is the mean proportional between x and z; show that 𝑥𝑦 + 𝑦𝑧 is the mean proportional between 𝑥² + 𝑦² and 𝑦² + 𝑧².
Solution:
It is given that,
The mean proportion between 𝑥 and 𝑧 is 𝑦
𝑦² = 𝑥𝑧
Need to prove,
𝑥𝑦 + 𝑦𝑧 is the mean proportional between 𝑥² + 𝑦² and 𝑦² + 𝑧²
(𝑥𝑦 + 𝑦𝑧)² = (𝑥² + 𝑦²)(𝑦² + 𝑧²)
Now,
In the LHS side it is given that,
(𝑥𝑦 + 𝑦𝑧)² = [𝑦(𝑥 + 𝑧)²]
(𝑥𝑦 + 𝑦𝑧)² = 𝑦2(𝑥 + 𝑧)²
(𝑥𝑦 + 𝑦𝑧)² = 𝑥𝑧(𝑥 + 𝑧)²
In the RHS side it is given that,
(𝑥² + 𝑦²)(𝑦² + 𝑧²) = (𝑥² + 𝑥𝑦)(𝑥𝑦 + 𝑧²)
(𝑥² + 𝑦²)(𝑦² + 𝑧²) = 𝑥(𝑥 + 𝑧)𝑧(𝑥 + 𝑧)
(𝑥² + 𝑦²)(𝑦² + 𝑧²) = 𝑥𝑧(𝑥 + 𝑧)²
LHS = RHS
Hence proved

Question 10. If q is the mean proportional between p and r, show that: 𝑝𝑞𝑟(𝑝 + 𝑞 + 𝑟)³ = (𝑝𝑞 + 𝑞𝑟 + 𝑟𝑝)³.
Solution:
It is given that,
The mean proportional between 𝑝 and 𝑟 is 𝑞
𝑞² = 𝑝𝑟
Now,
In the LHS side it is given that,
𝑝𝑞𝑟(𝑝 + 𝑞 + 𝑟)³ = 𝑞𝑞²(𝑝 + 𝑞 + 𝑟)³
𝑝𝑞𝑟(𝑝 + 𝑞 + 𝑟)³ = 𝑞³(𝑝 + 𝑞 + 𝑟)³
𝑝𝑞𝑟(𝑝 + 𝑞 + 𝑟)³ = [𝑞(𝑝 + 𝑞 + 𝑟)³
𝑝𝑞𝑟(𝑝 + 𝑞 + 𝑟)³ = (𝑝𝑞 + 𝑞² + 𝑞𝑟)³
(𝑝𝑞 + 𝑞² + 𝑞𝑟)³ = (𝑝𝑞 + 𝑞² + 𝑞𝑟)³
LHS = RHS
Hence proved

Question 11. If three quantities are in continued proportion; show that the ratio of the first to the third is the duplicate ratio of the first to the second.
Solution:
Let us assumed that,
𝑥, 𝑦 and 𝑧 be the three quantities which are in continued proportion
𝑦² = 𝑥𝑧_(1)
Now,
We need to prove that,
𝑥: 𝑧 = 𝑥²: 𝑦²
𝑥𝑦² = 𝑥²𝑧
In the LHS side it is given that,
𝑥𝑦² = 𝑥(𝑥𝑧) = 𝑥²𝑧
LHS = RHS
Hence proved.

Question 12. If y is the mean proportional between 𝑥 and 𝑧,

Question 13. Given four quantities a, b, c and d are in proportion. Show that:
(𝑎 − 𝑐)𝑏²: (𝑏 − 𝑑)𝑐𝑑 = (𝑎² − 𝑏² − 𝑎𝑏): (𝑐² − 𝑑² − 𝑐𝑑)
Solution:
It is given that,
a, b, c and d are proportion
Let us assumed that,
𝑎/𝑏 = 𝑐/𝑑 = 𝑘
By cross-multiplication,
𝑎 = 𝑏𝑘 𝑎𝑛𝑑 𝑐 = 𝑑𝑘
Now
In the LHS side it is given that,

Question 14. Find two numbers such that the mean proportional between them is 12 and the third proportional to them is 96.
Solution:
Let us assumed that,
a and b are the two numbers whose mean proportional is 12.
𝑎𝑏 = (12)²
𝑎𝑏 = 144
𝑏 = 144/𝑎 __(1)
It is given that,
The third proportional is 96
𝑎: 𝑏: : 𝑏: 96
𝑏² = 96𝑎
Put the value of b

Question 15. Find the third proportional of

Question 16. If 𝑝: 𝑞 = 𝑟: 𝑠; then show that: 𝑚𝑝 + 𝑛𝑞: 𝑞 = 𝑚𝑟 + 𝑛𝑠: 𝑠.
Solution:
It is given that,

Question 17. If  and

Question 19. If a, b, c and d are in proportion, prove that

Exercise 7C

Question 1. If 𝑎: 𝑏 = 𝑐: 𝑑, prove that:
(𝑖) 5𝑎 + 7𝑏: 5𝑎– 7𝑏 = 5𝑐 + 7𝑑: 5𝑐– 7𝑑.
(𝑖𝑖) (9𝑎 + 13𝑏) (9𝑐– 13𝑑) = (9𝑐 + 13𝑑)(9𝑎– 13𝑏).
(𝑖𝑖𝑖) 𝑥𝑎 + 𝑦𝑏: 𝑥𝑐 + 𝑦𝑑 = 𝑏 ∶ 𝑑.
Solution:

Question 2. If 𝑎: 𝑏 = 𝑐: 𝑑, prove that: (6𝑎 + 7𝑏)(3𝑐– 4𝑑) = (6𝑐 + 7𝑑)(3𝑎– 4𝑏).
Solution:
It is given that,

Question 5. If (7𝑎 + 8𝑏)(7𝑐– 8𝑑) = (7𝑎– 8𝑏)(7𝑐 + 8𝑑), prove that 𝑎: 𝑏 = 𝑐: 𝑑.
Solution:
It is given that,

Question 7. If (𝑎 + 𝑏 + 𝑐 + 𝑑) (𝑎– 𝑏– 𝑐 + 𝑑) = (𝑎 + 𝑏– 𝑐– 𝑑)(𝑎– 𝑏 + 𝑐– 𝑑), prove that 𝑎: 𝑏 = 𝑐: 𝑑.
Solution:
It is given that,
(𝑎 + 𝑏 + 𝑐 + 𝑑)(𝑎– 𝑏– 𝑐 + 𝑑) = (𝑎 + 𝑏– 𝑐– 𝑑)(𝑎– 𝑏 + 𝑐– 𝑑)

Question 9. If (𝑎² + 𝑏²) (𝑥² + 𝑦²) = (𝑎𝑥 + 𝑏𝑦)²; prove that: 𝑎/𝑥 = 𝑏/𝑦.
Solution:
It is given that,
(𝑎² + 𝑏²) (𝑥² + 𝑦²) = (𝑎𝑥 + 𝑏𝑦)²
𝑎²𝑥² + 𝑎²𝑦² + 𝑏²𝑥² + 𝑏²𝑦² = 𝑎2𝑥² + 2𝑎𝑥𝑏𝑦+𝑏²𝑦²
𝑎²𝑦² + 𝑏²𝑥² = 2𝑎𝑥𝑏𝑦
𝑎²𝑦² + 𝑏²𝑥² − 2𝑎𝑥𝑏𝑦 = 0
(𝑎𝑦 − 𝑏𝑥)² = 0
𝑎𝑦 − 𝑏𝑥 = 0
𝑎𝑦 = 𝑏𝑥
𝑎/𝑥 = 𝑏/𝑦
Hence proved

Question 10. If a, b and c are in continued proportion, prove that:

Question 11. Using properties of proportion, solve for :

Exercise 7D

Question 1. If 𝑎: 𝑏 = 3: 5, find: (10𝑎 + 3𝑏): (5𝑎 + 2𝑏)
Solution:
It is given that,
𝑎: 𝑏 = 3: 5

Question 2. If 5𝑥 + 6𝑦: 8𝑥 + 5𝑦 = 8: 9, find 𝑥: 𝑦.
Solution:
It is given that

Hence, the value of 𝑥: 𝑦 is 14: 19.

Question 3. If (3𝑥– 4𝑦): (2𝑥– 3𝑦) = (5𝑥– 6𝑦): (4𝑥– 5𝑦), find 𝑥: 𝑦.
Solution:
It is given that,
(3𝑥– 4𝑦): (2𝑥– 3𝑦) = (5𝑥– 6𝑦): (4𝑥– 5𝑦)

Question 4. Find the:
(i) duplicate ratio of 2√2: 3√5
(ii) triplicate ratio of 2𝑎: 3𝑏
(iii) sub-duplicate ratio of 9𝑥²𝑎⁴: 25𝑦⁶𝑏²
(iv) sub-triplicate ratio of 216: 343
(v) reciprocal ratio of 3: 5
(vi) ratio compounded of the duplicate ratio of 5: 6, the reciprocal ratio of 25: 42 and the sub duplicate ratio of 36: 49.
Solution:
(i) Duplicate ratio of 2√2: 3√5
(2√2)²: (3√5)²
(2 × 2 × √2 × √2): (3 × 3 × √5 × √5)
8: 45
Hence, the duplicate ratio of 2√2: 3√5 is 8: 45.
(ii) Triplicate ratio of 2𝑎: 3𝑏
(2𝑎)³: (3𝑏)³
(2 × 2 × 2 × 𝑎 × 𝑎 × 𝑎): (3 × 3 × 3 × 𝑏 × 𝑏 × 𝑏 )
8𝑎³: 27𝑏³
Hence, the triplicate ratio of 2𝑎: 3𝑏 is 8𝑎³: 27𝑏³.
(iii) Sub-duplicate ratio of 9𝑥²𝑎⁴: 25𝑦⁶𝑏²

Hence, the Sub-triplicate ratio of 216: 343 is 6: 7.
(v) Reciprocal ratio of 3: 5
5: 3
Hence, the reciprocal ratio of 3: 5 is 5: 3.
(vi) ratio compounded of the duplicate ratio of 5: 6, the reciprocal ratio of 25: 42 and the sub-duplicate
ratio of 36: 49.
Duplicate ratio of 5: 6
(5)²: (6)²
25: 36
Reciprocal ratio of 25: 42
42: 25
Sub-duplicate ratio of 36: 49
√36: √49
6: 7

Question 5. Find the value of x, if:
(i) (2𝑥 + 3): (5𝑥– 38) is the duplicate ratio of √5: √6
(ii) (2𝑥 + 1): (3𝑥 + 13) is the sub-duplicate ratio of 9: 25.
(iii) (3𝑥– 7): (4𝑥 + 3) is the sub-triplicate ratio of 8: 27.
Solution:
(i) (2𝑥 + 3): (5𝑥– 38) is the duplicate ratio of √5: √6 It is given that,
Duplicate ratio of √5: √6
Duplicate ratio of (√5)²: (√6)²
The duplicate ratio is 5: 6

By cross-multiplication,
6(2𝑥 + 3) = 5(5𝑥 − 38)
12𝑥 + 18 = 25𝑥 − 190
12𝑥 − 25𝑥 = −190 − 18
−13𝑥 = −208
13𝑥 = 208
𝑥 = 208/13
𝑥 = 16
Hence, the value of 𝑥 is 16
(ii) (2𝑥 + 1): (3𝑥 + 13) is the sub-duplicate ratio of 9: 25.
It is given that,
Sub-duplicate ratio of 9: 25
Sub-duplicate ratio of √9: √25
The sub-duplicate ratio is 3: 5

By cross-multiplication,
5(2𝑥 + 1) = 3(3𝑥 + 13)
10𝑥 + 5 = 9𝑥 + 39
10𝑥 − 9𝑥 = +39 − 5
𝑥 = 39 − 5
𝑥 = 34
Hence, the value of 𝑥 is 34.
(iii) (3𝑥– 7): (4𝑥 + 3) is the sub-triplicate ratio of 8: 27.
It is given that,
Sub-duplicate ratio of 8: 27
Sub-duplicate ratio of 3√8 : 3√27
The sub-duplicate ratio is 2: 3

By cross-multiplication,
3(3𝑥 − 7) = 2(4𝑥 + 3)
9𝑥 − 21 = 8𝑥 + 6
9𝑥 − 8𝑥 = 6 + 21
𝑥 = 27
Hence, the value of 𝑥 is 27.

Question 6. What quantity must be added to each term of the ratio 𝑥: 𝑦 so that it may become equal to 𝑐: 𝑑?
Solution:
Let us assumed that,
The quantity which is to be added be a.
𝑥+𝑎/𝑦+𝑝 = 𝑐/𝑑
By cross multiplication,
𝑑(𝑥 + 𝑝) = 𝑐(𝑦 + 𝑝)
𝑑𝑥 + 𝑝𝑑 = 𝑐𝑦 + 𝑐𝑝
𝑝𝑑 − 𝑐𝑝 = 𝑐𝑦 − 𝑑𝑥
𝑝(𝑑 − 𝑐) = 𝑐𝑦 − 𝑑𝑥

Question 7. A woman reduces her weight in the ratio 7: 5. What does her weight become if originally it was 84 kg?
Solution:
It is given that,
Original weight is 84kg
Let us assumed that,
The reduced weight is 𝑥
84: 𝑥 = 7: 5
84/𝑥 = 7/5
By cross multiplication,
84 × 5 = 7 × 𝑥
84×5/7 = 𝑥
12 × 5 = 𝑥
60 = 𝑥
𝑥 = 60
Hence, reduced weight us 60 kg.

Question 8. If 15(2𝑥²– 𝑦²) = 7𝑥𝑦, find 𝑥: 𝑦; if x and y both are positive.
Solution:
It is given that,
15(2𝑥²– 𝑦²) = 7𝑥𝑦
By substitution,

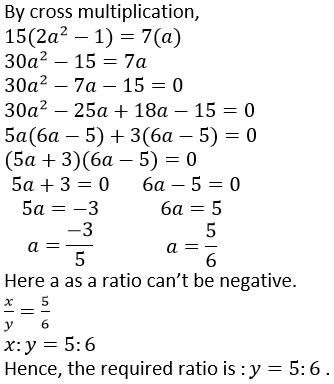
Question 9. Find the:
(i) fourth proportional to 2𝑥𝑦, 𝑥² and 𝑦².
(ii) third proportional to 𝑎²– 𝑏² and 𝑎 + 𝑏.
(iii) mean proportional to (𝑥– 𝑦) and (𝑥³– 𝑥²𝑦).
Solution:
(i) Let us assumed that,
Fourth proportional to 2𝑥𝑦, 𝑥² and 𝑦² be 𝑛.
2𝑥𝑦: 𝑥² = 𝑦²: 𝑛

Question 10. Find two numbers such that the mean proportional between them is 14 and third proportional to them is 112.
Solution:
It is given that,
Mean proportional between numbers is 14
Let us assumed that,
The two number are 𝑎 and 𝑏
Now,
𝑎: 14 = 14: 𝑏
𝑎/14 = 14/𝑏
By cross multiplication,
𝑎 × 𝑏 = 14 × 14
𝑎𝑏 = 196
𝑎 = 196/𝑏__________________________(1)
The third proportional to 𝑎 and 𝑏 is 112.
𝑎: 𝑏 = 𝑏: 112
𝑎/𝑏 = 𝑏/112
𝑎 × 112 = 𝑏 × 𝑏
𝑏2 = 𝑎112 __________________________(2)

Put the value of a in above equation,
𝑏² = 196/𝑏 × 112
𝑏² × 𝑏 = 196 × 112
𝑏³ = 196 × 112
𝑏³ = 21952
𝑏 = 28
Put the value of 𝑎 in equation 2
𝑎 = 196/28
𝑎 = 7
Hence, the required two numbers are 7 and 28.

Question 11. If x and y be unequal and 𝑥: 𝑦 is the duplicate ratio of 𝑥 + 𝑧 and 𝑦 + 𝑧, prove that z is mean proportional between x and y.
Solution:
It is given that,

By cross multiplication,
𝑥(𝑦² + 2𝑦𝑧 + ^𝑧2) = 𝑦(𝑥² + 2𝑥𝑧 + 𝑧²)
𝑥𝑦² + 2𝑥𝑦𝑧 + 𝑥𝑧² = 𝑦𝑥² + 2𝑥𝑦𝑧 + 𝑦𝑧²
𝑥𝑦² + 𝑥𝑧² = 𝑦𝑥² + 𝑦𝑧²
𝑥𝑦² − 𝑥²𝑦 = 𝑦𝑧² − 𝑥𝑧²
𝑥𝑦(𝑦 − 𝑥) = 𝑧²(𝑦 − 𝑥)
𝑥𝑦 = 𝑧²
Hence, the mean proportional between 𝑥 and 𝑦 is 𝑧

Question 13. If (4𝑎 + 9𝑏)(4𝑐– 9𝑑) = (4𝑎– 9𝑏)(4𝑐 + 9𝑑), prove that: 𝑎: 𝑏 = 𝑐: 𝑑.
Solution:
It is given that,
(4𝑎 + 9𝑏)(4𝑐– 9𝑑) = (4𝑎– 9𝑏)(4𝑐 + 9𝑑)

Question 15. There are 36 members in a student council in a school and the ratio of the number of boys to the number of girls is 3: 1. How any more girls should be added to the council so that the ratio of the number of boys to the number of girls may be 9: 5?
Solution:
It is given that,
Ratio of number of boys to the number of girls = 3: 1
Let us assumed that,
The number of boys be 3𝑥
Number of girls be 𝑥
3𝑥 + 𝑥 = 36
4𝑥 = 36
𝑥 = 9
Number of boys = 3𝑥 = 27
Number of girls = 𝑥 = 9
Let us assumed that,
Number of girls be added to the council = 𝑛
We have:
27/9+𝑛 = 9/𝑛
By Cross multiplication,
27 × 5 = 9(9 + 𝑛)
135 = 81 + 9𝑛
−9𝑛 = 81 − 135
−9𝑛 = −54
𝑛 = 6
Hence, the council has added 6 girls.

Question 16. If 7𝑥– 15𝑦 = 4𝑥 + 𝑦, find the value of 𝑥: 𝑦. Hence, use componendo and dividend to find the values of:

Question 21. Using componendo and dividend find the value of

By cross multiplication,
(𝑥 + 1)²(𝑎 − 1) = (𝑥 − 1)²(𝑎 + 1)
(𝑥² + 2𝑥 + 1)(𝑎 − 1) = (𝑥² − 2𝑥 + 1)(𝑎 + 1)
𝑎(𝑥² + 2𝑥 + 1) − (𝑥² + 2𝑥 + 1) = 𝑎(𝑥² − 2𝑥 + 1) + (𝑥² − 2𝑥 + 1)
𝑎𝑥² + 2𝑎𝑥 + 𝑎 − 𝑥² − 2𝑥 − 1 = 𝑎𝑥² − 2𝑎𝑥 + 𝑎 + 𝑥² − 2𝑥 + 1
2𝑎𝑥 − 𝑥² − 1 = −2𝑎𝑥 + 𝑥² + 1
2𝑎𝑥 − 𝑥² − 1 + 2𝑎𝑥 − 𝑥² − 1 = 0
4𝑎𝑥 − 2𝑥² − 2 = 0
2(2𝑎𝑥 − 𝑥² − 1) = 0
2𝑎𝑥 − 𝑥² − 1 = 0
Hence proved.

Question 27. Simplification:- (2𝑥² − 5𝑦²): 𝑥𝑦 = 1: 3
Solution:
It is given that,
(2𝑥² − 5𝑦²): 𝑥𝑦 = 1: 3

By cross multiplication,
3(2𝑎³ − 5) = 𝑎
6𝑎³ − 15 = 𝑎
6𝑎³ − 𝑎 − 15 = 0
By splitting the middle term,
6𝑎³ + 9𝑎 − 10𝑎 − 15 = 0
3𝑎(2𝑎³ + 3) − 5(2𝑎 + 3) = 0
(3𝑎 − 5)(2𝑎 + 3) = 0
(3𝑎 − 5) = 0 (2𝑎 + 3) = 0
3𝑎 − 5 = 0            2𝑎 + 3 = 0
3𝑎 = 5                   2𝑎 = −3
𝑎 = 5/3                  𝑎 = − 3/2
a can’t be negative so, 𝑎 = 5/3
𝑥/𝑦 = 𝑎
𝑥/𝑦 = 5/3
𝑥: 𝑦 = 5: 3
Hence, the ratio of 𝑥: 𝑦 is 5: 3

Question 30. If a, b and c are in continued proportion, prove that: 𝑎: 𝑐 = (𝑎² + 𝑏²): (𝑏² + 𝑐²)
Solution:
It is given that,
a, b and c are in continued proportion
𝑎: 𝑏 = 𝑏: 𝑐
Let us assumed that,
𝑎/𝑏 = 𝑏/𝑐 = 𝑘
By cross multiplication,
𝑎 = 𝑏𝑘, 𝑏 = 𝑐𝑘
𝑎 = 𝑐𝑘 × 𝑘
𝑎 = 𝑐𝑘²
Now,
In the LHS side it is given that,