Selina ICSE Class 10 Maths Solutions Chapter 9 Matrices

Question 1. State, whether the following statements are true or false. If false, give a reason.
(i) If A and B are two matrices of orders 3 × 2 and 2 × 3 respectively; then their sum A + B is possible.
(ii) The matrices A2 × 3 and B2 × 3 are conformable for subtraction.
(iii) Transpose of a 2 × 1 matrix is a 2 × 1 matrix.
(iv) Transpose of a square matrix is a square matrix.
Solution:
(i) False, When the order of both matrices A and B is the same, the total A + B is achievable.
(ii) True
(iii) False, A 1×2 matrix is the transpose of a 2×1 matrix.
(iv) True
(v) False, There is only one column in a column matrix, yet there are numerous rows.

Question 2. Given:

Here matrices are equal then corresponding elements are equal.
𝑥 = 3________(𝑖)
𝑦 + 2 = 1
𝑦 = −1________(𝑖𝑖)
𝑧 – 1 = 2
𝑧 = 3________(𝑖𝑖𝑖)
Hence, the value of 𝑥, 𝑦 and 𝑧 is 3, -1 and 3.

Question 3. Solve for a, b and c if

Matrices are equal then corresponding elements are equal.
𝑎 + 5 = 2_______(𝑖)
𝑎 = −3
−4 = 𝑏 + 4
𝑏 = −8__________(𝑖𝑖)
2 = 𝑐– 1
𝑐 = 3__________(𝑖𝑖𝑖)
Hence, the value of 𝑥, 𝑦 and 𝑧 is -3, -8 and 3 respectively.
(ii) We have,

Matrices are equal then corresponding elements are equal.
𝑎 = 3____________(𝑖)
𝑎 − 𝑏 = −1____________(𝑖𝑖)
𝑏 + 𝑐 = 2____________(𝑖𝑖𝑖)
From equation (ii) we get,
𝑎 − 𝑏 = −1
3 − 𝑏 = −1
−𝑏 = −1 − 3
−𝑏 = −4
𝑏 = 4
From equation (iii) we get,
𝑏 + 𝑐 = 2
4 + 𝑐 = 2
𝑐 = 2 − 4
𝑐 = −2
Hence, the value of a, b and c is 3, 4 and -2 respectively.

Question 4. If 𝐴 = [8 −3] and 𝐵 = [4 −5]; find:
(𝑖)𝐴 + 𝐵
(𝑖𝑖) 𝐵– 𝐴
Solution:
(i) 𝐴 + 𝐵
[8 −3] + [4 −5]
[8 + 4 −3 − 5]
[12 −8]
Hence, the value of 𝐴 + 𝐵 is [12 −8].
(ii) 𝐵 − 𝐴
[4 −5] − [8 −3]
[4 − 8 −5 − (−3)]
[−4 −5 + 3]
[−4 −2]
Hence, the value of 𝐵 − 𝐴 is [−4 −2].

Question 5. If

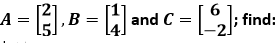
(𝑖) 𝐵 + 𝐶
(𝑖𝑖) 𝐴 − 𝐶
(𝑖𝑖𝑖) 𝐴 + 𝐵 − 𝐶
(𝑖𝑣) 𝐴 − 𝐵 + 𝐶
Solution:
(i) It is given that,

Question 6. Wherever possible, write each of the following as a single matrix.

Question 7. Find x and y from the following equations:

Matrices are equal then corresponding elements are equal.
3 − 𝑥 = 7____________(i)
𝑦 − 4 = 2____________(ii)
From equation (i) we get,
−𝑥 = 7 − 3
−𝑥 = 4
𝑥 = −4
From equation (ii) we get,
𝑦 − 4 = 2
𝑦 = 2 + 4
𝑦 = 6
Hence, the value of x and y is -4 and 6 respectively.

Question 8. Given:

Question 9. Write the additive inverse of matrices A, B and C:

Question 10. Given A = [2 −3], B = [0 2] and C = [−1 4]; find the matrix X in each of the following:
(𝑖) 𝑋 + 𝐵 = 𝐶 − 𝐴
(𝑖𝑖) 𝐴 − 𝑋 = 𝐵 + 𝐶
Solution:
It is given that,
A = [2 −3], B = [0 2] and C = [−1 4]
(i) X + B = C − A
Put the value of A, B and C.

Question 11. Given A =

Exercise 9B

Question 1. Evaluate

Question 2. Find x and y if:

Solution:
(i) 3[4 𝑥] + 2[𝑦 −3] = [10 0]
[12 3𝑥] + [2𝑦 −6] = [10 0]
[12 + 2𝑦 3𝑥 + (−6)] = [10 0]
By comparing,
12 + 2𝑦 = 10_____________(𝑖)
3𝑥 − 6 = 0_____________(𝑖𝑖)
From equation (i) we get,
12 + 2𝑦 = 10
2𝑦 = 10 − 12
2𝑦 = −2
𝑦 = −2/2
𝑦 = −1
From equation (ii) we get,
3𝑥 = 6
𝑥 = 6/3
𝑥 = 2
Hence, the value of x and y is 2 and -1.

Question 3. Given

Question 4. If

Question 5. Given

Question 6. If

By comparing both the matrix is we get,
2𝑥 + 9 = −7_______________(𝑖)
3𝑦 = 15_______________(𝑖𝑖)
𝑧 = 9_______________(𝑖𝑖𝑖)
From equation (i) we get,
2𝑥 = −7 − 9
2𝑥 = −16
𝑥 = −8
From equation (ii) we get,
3𝑦 = 15
𝑦 = 15/3
𝑦 = 5
Hence, the value of 𝑥, 𝑦 and 𝑧 are -8, 5 and 9 respectively.

Question 7. Given

Question 8. Given

Question 9. If

Question 10. If I is the unit matrix of order 2×2; find the matrix M, such that:

Question 11. If

Exercise 9C

Question 1. Evaluate: If possible:

In the given matrix number of columns does not equal the number of rows in the second matrix. Hence, product can’t be possible.

Question 2. If

Question 3. If

4𝑥 = 16____________(𝑖)
1 = −𝑦__(𝑖𝑖)
From equation (i) we get,
4𝑥 = 16
𝑥 = 16
4
𝑥 = 4
From equation (ii) we get,
1 = −𝑦
𝑦 = −1
Hence, the value of x and y is 4 and -1 respectively.

Question 4. Find x and y, if:

By comparing both the sides,
20 + 3𝑥 = 𝑦(𝑖)
5𝑥 − 2 = 8___________(𝑖𝑖)
From equation (𝑖𝑖) get the value of 𝑥
5𝑥 − 2 = 8
5𝑥 = 8 + 2
5𝑥 = 10
𝑥 = 10/5
𝑥 = 2
Put the value of x in equation (i)
20 + 3(2) = 𝑦
20 + 6 = 𝑦
26 = 𝑦
𝑦 = 26
Hence, the value of x and y is 2 and 26 respectively.

Question 5. If

Question 6. Given

(iii) Because the number of columns in matrix A is not equal to the number of rows, the product AA=A^2 is not possible.

Question 7. Let

Question 8. If

Question 9. If

Question 10. Given

Question 11. If

Question 12. Find the matrix A, if

Question 13. If

By comparing,
1 + 𝑎 = 1_____________(𝑖)
𝑎 + 𝑏² = 1___________(𝑖𝑖)
From equation (i),
1 + 𝑎 = 1
𝑎 = 1 − 1
𝑎 = 0
Put the value of a in equation (𝑖𝑖)
𝑎 + 𝑏² = 1
0 + 𝑏² = 1
𝑏² = 1
𝑏 = 1

Question 14. If

Question 15. If

Question 16 (i). Solve for x and

Question 16 (ii). Solve for x and y:

Question 16 (iii). Solve for x and y:

By comparing both matrix,
−4 = 2𝑦___(𝑖)
2𝑥 = 6_______________(𝑖𝑖)
From equation (i) we get, the value of 𝑦
2𝑦 = −4
𝑦 = −4/2
𝑦 = −2
From equation (ii) we get, the value of 𝑥
2𝑥 = 6
𝑥 = 6/2
𝑥 = 3
Hence, the value of x and y is 3 and -2.

Question 17. In each case given below, find:
(a) The order of matrix M.
(b) The matrix M.

[𝑎 + 0 𝑎 + 2𝑏] = [1 2]
By comparing
𝑎 + 0 = 1__________(𝑖)
𝑎 + 2𝑏 = 2__________(𝑖𝑖)
From equation (i) we get,
𝑎 = 1
Put the value of a in equation (ii),
1 + 2𝑏 = 2
2𝑏 = 2 − 1
2𝑏 = 1
𝑏 = 1/2
Hence, the value of a and b is 1 and 1/2.

By comparing both the matrix,
𝑎 + 4𝑏 = 13___________________(𝑖)
2𝑎 + 𝑏 = 5 _______(𝑖𝑖)
From equation (i) we get,
𝑎 + 4𝑏 = 13
𝑎 = 13 − 4𝑏_______(𝑖𝑖𝑖)
Value of a put in equation (ii)
2(13 − 4𝑏) + 𝑏 = 5
26 − 8𝑏 + 𝑏 = 5
26 − 7𝑏 = 5
−7𝑏 = 5 − 26
−7𝑏 = −21
𝑏 = −21/−7
𝑏 = 3
Put the value of b in equation (iii)
𝑎 = 13 − 4(3)
𝑎 = 13 − 12
𝑎 = 1
Hence, the value of a and b is 1 and 3.

Question 18. If

Question 19. If

Question 20. If A and B are any two 2 × 2 matrices such that 𝐴𝐵 = 𝐵𝐴 = 𝐵 and B is not a zero matrix, what can you say about the matrix A?
Solution:
It is given that,
𝐴𝐵 = 𝐵𝐴 = 𝐵
We know that, 𝐴𝐼 = 𝐼𝐴, with I being the identified matrix.
As a result, B stands for the identified matrix.

Question 21. Given

By comparing,
3𝑎 = 3 + 𝑎__(𝑖)
3𝑏 + 0 = 𝑏__(𝑖𝑖)
4𝑐 = 4 + 𝑐__(𝑖𝑖𝑖)
From equation (i) we get,
3𝑎 − 𝑎 = 3
2𝑎 = 3
𝑎 = 3/2
From equation (ii) we get,
3𝑏 + 0 = 𝑏
3𝑏 − 𝑏 = 0
𝑏 = 0
From equation (iii) we get,
4𝑐 = 4 + 𝑐
4𝑐 − 𝑐 = 4
3𝑐 = 4
𝑐 = 4/3
Hence, the value of a, b and c is 3/2, 0 and 4/3.

Question 22. If

Question 23. Given the matrices:

Question 24. If

Question 25. If

Question 26. If

Question 27. If

Question 28. If

Question 29. If

By comparing,
6+6y=0____________(i)
2x+12=0____________(ii)
From equation (i) we get,
6+6y=0
6y=-6
y=-6/6
y=-1
From equation (ii) we get,
2x+12=0
2x=-12
x=-12/2
x=-6
Hence, the value x and y is -1 and -6.

Question 30. Evaluation without using tables:

Question 31. State, with reason, whether the following are true or false. A, B and C are matrices of order 2 × 2.
(𝑖) 𝐴 + 𝐵 = 𝐵 + 𝐴
(𝑖𝑖) 𝐴 – 𝐵 = 𝐵 – 𝐴
(𝑖𝑖𝑖) (𝐵. 𝐶). 𝐴 = 𝐵. (𝐶. 𝐴)
(𝑖𝑣) (𝐴 + 𝐵). 𝐶 = 𝐴. 𝐶 + 𝐵. 𝐶
(𝑣) (𝐵 – 𝐶) = 𝐴. 𝐵 – 𝐴. 𝐶
(𝑣𝑖) (𝐴 – 𝐵). 𝐶 = 𝐴. 𝐶 – 𝐵. 𝐶
(𝑣𝑖𝑖) 𝐴² – 𝐵² = (𝐴 + 𝐵) (𝐴 – 𝐵)
(𝑣𝑖𝑖𝑖) (𝐴 – 𝐵)² = 𝐴² – 2𝐴. 𝐵 + 𝐵²
Solution:
(i) True matrices addition is commutative.
(ii) False matrices subtraction is commutative.
(iii) True matrices multiplication is associative.
(iv) True matrices multiplication is distributive over addition.
(v) True matrices multiplication is distributive over subtraction.
(vi) Matrix multiplication is distributive when compared to subtraction.
(vii) For factorization and expansion, the False Laws of Algebra do not apply to matrices.
(viii) For factorization and expansion, the False Laws of Algebra do not apply to matrices.

Exercise 9D

Question 1. Find x and y if:

By comparing,
6𝑥 − 10 = 8____________(𝑖)
−2𝑥 + 14 = 4𝑦_(𝑖𝑖)
From equation (i) we get,
6𝑥 − 10 = 8
6𝑥 = 8 + 10
6𝑥 = 18
𝑥 = 18/6
𝑥 = 3
Put the value of x in equation (𝑖𝑖)
−2𝑥 + 14 = 4𝑦
−2(3) + 14 = 4𝑦
−6 + 14 = 4𝑦
−8 = 4𝑦/
8/4 = 𝑦
𝑦 = 2

Question 2. Find x and 𝑦, if:

[3𝑥 + 24   12𝑥 + 56] − [6 −21] = [15 10𝑦]
[3𝑥 + 24 − 6   12𝑥 + 56 − (−21)] = [15 10𝑦]
[3𝑥 + 18   12𝑥 + 77] = [15 10𝑦]
By comparing,
3𝑥 + 18 = 15_________(𝑖)
12𝑥 + 77 = 10𝑦_(𝑖)
From equation (i) we get,
3𝑥 + 18 = 15
3𝑥 = 15 − 18
3𝑥 = −3
𝑥 = − 3/3
𝑥 = −1

Question 3. If

(i) 𝑥, 𝑦 ∈ 𝑊 (whole number)
It can be observed that the above two equations are satisfied when 𝑥 = 3 and 𝑦 = 4.
(ii) 𝑥, 𝑦 ∈ 𝑍 (integers)
It can be observed that the above two equations are satisfied when 𝑥 = ±3 and 𝑦 = ±4.

Question 4. Given

Question 5. Evaluate:

Question 6. If

Question 7. If

By comparing,
𝑎 + 1 = 5______________(𝑖)
2 + 𝑏 = 0______________(𝑖𝑖)
−1 − 𝑐 = 3____________(𝑖𝑖𝑖)
Form equation (i) we get,
𝑎 = 5 − 1
𝑎 = 4
Form equation (ii) we get,
2 + 𝑏 = 0
𝑏 = −2
Form equation (iii) we get,
−𝑐 = 3 + 1
−𝑐 = 4
𝑐 = −4
Hence, the value of a, b and c is 4, -2 and -4.

Question 8. If 𝐴 =