Get ICSE Class 10 Physics syllabus for your exam. Every student should know the syllabus of a particular subject before attending that exam. To solve this problem, we provide you ICSE Class 10 Physics syllabus for your exam
It is hard to imagine to make preparation for class 10 physics without ICSE Class 10 Physics syllabus So if you want to score higher marks in your exam. So, firstly learn the ICSE Class 10 Physics syllabus, and then let’s start to practice in class 10 physics.
ICSE Class 10 Physics syllabus
1. Force, Work, Power and Energy
(i) Turning forces concept; moment of a force; forces in equilibrium; centre of gravity; [discussions
using simple examples and simple numerical problems].
Elementary introduction of translational and rotational motions; moment (turning effect) of a force,
also called torque and its cgs and SI units; common examples—door, steering wheel, bicycle pedal, etc.;
clockwise and anti-clockwise moments; conditions for a body to be in equilibrium ( translational and
rotational); principle of moment and its verification using a metre rule suspended by two spring balances
with slotted weights hanging from it; simple numerical problems; Centre of gravity (qualitative only) with
examples of some regular bodies and irregular lamina.
(ii) Uniform circular motion.
As an example of constant speed, though acceleration (force) is present. Differences between centrifugal and
centripetal force.
(iii) Work, energy, power and their relation with force.
Definition of work. W = FS cosq; special cases of q = 0°, 90°. W= mgh. Definition of energy, energy as
work done. Various units of work and energy and their relation with SI units.[erg, calorie, kW h and eV].
Definition of Power, P=W/t; SI and cgs units; other units, kilowatt (kW), megawatt (MW) and gigawatt
(GW); and horse power (1hp=746W) [Simple numerical problems on work, power and energy].
(iv) Different types of energy (e.g. chemical energy, Mechanical energy, heat energy, electrical energy,
nuclear energy, sound energy, light energy).
Mechanical energy: potential energy U = mgh (derivation included) gravitational PE, examples; kinetic energy K= ½ mv2 (derivation included); forms of kinetic energy: translational, rotational and vibrational – only simple examples. [Numerical problems on K and U only in case of translational motion]; qualitative discussions of electrical, chemical, heat, nuclear, light and sound energy, conversion from one form to another; common examples.
(v) Machines as force multipliers; load, effort, mechanical advantage, velocity ratio and efficiency; simple treatment of levers, pulley systems showing the utility of each type of machine.
Functions and uses of simple machines :
Terms—effort E, load L, mechanical advantage MA = L/E, velocity ratio VR = VE/VL = dE / dL, input (Wi), output (Wo), efficiency (h), relation between h and MA,VR (derivation included); for all practical machines h <1; MA < VR.
Lever : principle. First, second and third class of levers; examples: MA and VR in each case. Examples of each
of these classes of levers as also found in the human body.
Pulley system : single fixed, single movable, block and tackle; MA, VR and h in each case.
(vi) Principle of Conservation of energy.
Statement of the principle of conservation of energy; theoretical verification that U + K = constant for a
freely falling body. Application of this law to simple pendulum (qualitative only); [simple numerical problems].
2. Light
(i) Refraction of light through a glass block and a triangular prism – qualitative treatment of simple applications such as real and apparent depth of objects in water and apparent bending of sticks in water. Applications of refraction of light.
Partial reflection and refraction due to change in medium. Laws of refraction; the effect on speed (V), wavelength (l) and frequency (f) due to refraction of light; conditions for a light ray to pass undeviated. Values of speed of light (c) in vacuum, air water and glass; refractive index μ = c/V, V = fl. Values of μ for common substances such as water, glass and diamond; experimental verification; refraction through glass block; lateral displacement; multiple images in thick
glass plate/mirror; refraction through a glass prism simple applications: real and apparent depth of objects in water; apparent bending of a stick under water. (Simple numerical problems and approximate ray diagrams required).
(ii) Total internal reflection: Critical angle; examples in triangular glass prisms; comparison with
reflection from a plane mirror (qualitative only). Applications of total internal reflection.
Transmission of light from a denser medium (glass/ water) to a rarer medium (air) at different angles of
incidence; critical angle (C) μ = 1/sinC. Essential conditions for total internal reflection. Total internal
reflection in a triangular glass prism; ray diagram, different cases – angles of prism (60°,60°,60°),
(60°,30°,90°), (45°,45°,90°); use of right angle prism to obtain d = 90° and 180° (ray diagram); comparison
of total internal reflection from a prism and reflection from a plane mirror.
(iii) Lenses (converging and diverging) including characteristics of the images formed (using ray diagrams only); magnifying glass; location of images using ray diagrams and thereby determining magnification.
(iv) Types of lenses (converging and diverging), convex and concave, action of a lens as a set of prisms;
technical terms; centre of curvature, radii of curvature, principal axis, foci, focal plane and focal length,;
detailed study of refraction of light in spherical lenses through ray diagrams; formation of images – principal
rays or construction rays; location of images from ray diagram for various positions of a small linear object
on the principal axis; characteristics of images. Sign convention and direct numerical problems using the
lens formula are included.(derivation of formula not required)
Scale drawing or graphical representation of ray diagrams not required.
Power of a lens (concave and convex) – [simple direct numerical problems]: magnifying glass or simple
microscope: location of image and magnification from ray diagram only [formula and numerical problems
not included]. Applications of lenses.
(v) Using a triangular prism to produce a visible spectrum from white light; Electromagnetic
spectrum. Scattering of light.
Deviation produced by a triangular prism; dependence on colour (wavelength) of light; dispersion
and spectrum; electromagnetic spectrum: broad classification (names only arranged in order of
increasing wavelength); properties common to all electromagnetic radiations; properties and uses of
infrared and ultraviolet radiation. Simple application of scattering of light e.g. blue colour of the sky.
3. Sound
(i) Reflection of Sound Waves; echoes: their use; simple numerical problems on echoes.
Production of echoes, condition for formation of echoes; simple numerical problems; use of echoes by
bats, dolphins, fishermen, medical field. SONAR.
(ii) Natural vibrations, Damped vibrations, Forced vibrations and Resonance –
a special case of forced vibrations. Meaning and simple applications of natural, damped, forced vibrations and resonance.
(iii) Loudness, pitch and quality of sound:
Characteristics of sound: loudness and intensity; subjective and objective nature of these properties; sound level in db (as unit only); noise pollution; interdependence of: pitch and frequency; quality and waveforms (with examples).
4. Electricity and Magnetism
(i) Ohm’s Law; concepts of emf, potential difference, resistance; resistances in series and
parallel, internal resistance.
Concepts of pd (V), current (I), resistance (R) and charge (Q). Ohm’s law : statement, V=IR; SI units;
experimental verification; graph of V vs I and resistance from slope; ohmic and non-ohmic resistors, factors
affecting resistance (including specific resistance) and internal resistance; super conductors, electromotive
force (emf); combination of resistances in series and parallel and derivation of expressions for equivalent
resistance. Simple numerical problems using the above relations. [Simple network of resistors].
(ii) Electrical power and energy.
Electrical energy; examples of heater, motor, lamp, loudspeaker, etc. Electrical power; measurement of
electrical energy, W = QV = VIt from the definition of pd. Combining with ohm’s law W = VIt = I2 Rt =
(V2/R)t and electrical power P = (W/t) = VI = I2R = V2/R. Units : SI and commercial; Power rating of common
appliances, household consumption of electric energy; calculation of total energy consumed by electrical
appliances; W = Pt (kilowatt × hour = kW h), [simple numerical problems].
(iii) Household circuits – main circuit; switches;
fuses; earthing; safety precautions; three-pin plugs; colour coding of wires. House wiring (ring system), power distribution; main circuit (3 wires-live, neutral, earth) with fuse / MCB, main switch and its advantages – circuit diagram; two way switch, staircase wiring, need for earthing, fuse, 3-pin plug and socket; Conventional location of live, neutral and earth points in 3 pin plugs and sockets. Safety precautions, colour coding of wires.
(iv) Magnetic effect of a current (principles only, laws not required); electromagnetic induction
(elementary);
transformer. Oersted’s experiment on the magnetic effect of electric current; magnetic field (B) and field lines due to current in a straight wire (qualitative only), right hand thumb rule – magnetic field due to a current in
a loop; Electromagnets: their uses; comparisons with a permanent magnet; Fleming’s Left Hand Rule, the
DC electric motor- simple sketch of main parts (coil, magnet, split ring commutators and brushes); brief description and type of energy transfer(working not required): Simple introduction to electromagnetic induction; frequency of AC in house hold supplies, Fleming’s Right Hand Rule, AC Generator – Simple sketch of main parts, brief description and type of energy transfer(working not required). Advantage of AC over DC. Transformer- its types, characteristics of primary and secondary coils in each type (simple labelled diagram and its uses).
5. Heat
(i) Calorimetry : meaning, specific heat capacity;
principle of method of mixtures; Numerical Problems on specific heat capacity using heat
loss and gain and the method of mixtures.
Heat and its units (calorie, joule), temperature and its units (°C, K); thermal (heat) capacity C’ = Q/△T…
(SI unit of C): Specific heat Capacity C = Q/m△T (SI unit of C) Mutual relation between Heat Capacity
and Specific Heat capacity, values of C for some common substances (ice, water and copper). Principle
of method of mixtures including mathematical statement. Natural phenomenon involving specific
heat. Consequences of high sp. heat of water. [Simple numerical problem].
(ii) Latent heat; loss and gain of heat involving change of state for fusion only.
Change of phase (state); heating curve for water; latent heat; sp latent heat of fusion (SI unit). Simple
numerical problems. Common physical phenomena involving latent heat of fusion.
6. Modern Physics
(i) Radioactivity and changes in the nucleus;
background radiation and safety precautions. Brief introduction (qualitative only) of the nucleus,
nuclear structure, atomic number (Z), mass number (A).Radioactivity as spontaneous disintegration. a, ß
and γ – their nature and properties; changes within the nucleus. One example each of a and b decay
with equations showing changes in Z and A. Uses of radioactivity – radio isotopes. Harmful effects. Safety
precautions. Background radiation. Radiation : X-rays; radioactive fallout from nuclear plants and other sources. Nuclear Energy : working on safe disposal of waste. Safety measures to be strictly reinforced.
(ii) Nuclear fission and fusion; basic introduction and equations. SI units (System International d’Unites) were adopted
internationally in 1968.
Fundamental units : The system has seven fundamental (or basic) units, one for each of the fundamental quantities.
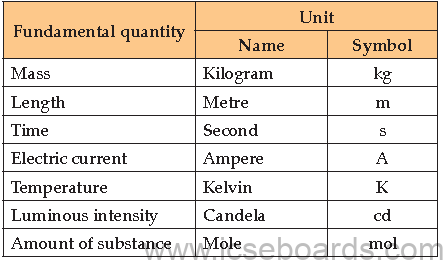
Derived units : These are obtained from the fundamental units by multiplication or division; no
numerical factors are involved. Some derived units with complex names are:
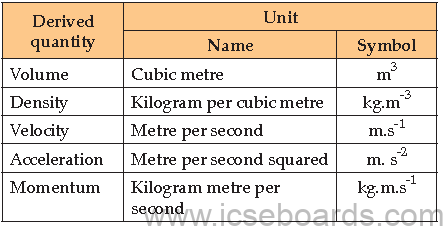
Some derived units are given special names due to their complexity when expressed in terms of the
fundamental units, as below:
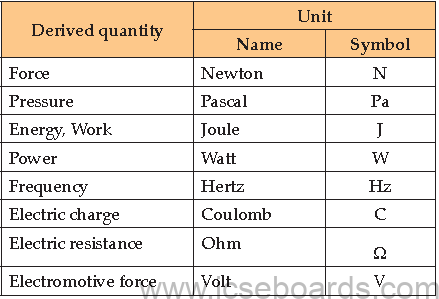
When the unit is named after a person, the symbol has a capital letter.
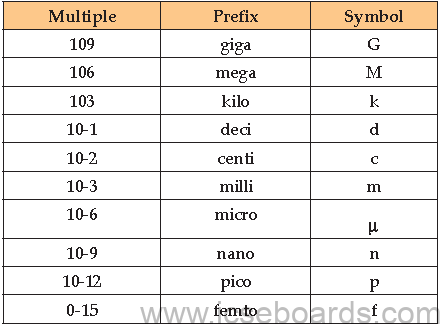
Standard prefixes : Decimal multiples and submultiples are attached to units when appropriate,
as below:
Internal Assessment of
Practical Work
Candidates will be asked to carry out experiments for which instructions will be given. The experiments may be
based on topics that are not included in the syllabus but theoretical knowledge will not be required. A candidate
will be expected to be able to follow simple instructions, to take suitable readings and to present these readings in a
systematic form. He/she may be required to exhibit his/her data graphically. Candidates will be expected to appreciate
and use the concepts of least count, significant figures and elementary error handling.
Note : Teachers may design their own set of experiments, preferably related to the theory syllabus. A comprehensive
list is suggested below.
1. Lever : There are many possibilities with a meter rule as a lever with a load (known or unknown)
suspended from a point near one end (say left), the lever itself pivoted on a knife edge, use slotted
weight Determine the mass of a metre rule using a spring balance or by balancing it on a knife edge at some point away from the middle and a 50g weight on the other side. Next pivot (F) the metre rule at the 40cm, 50cm and 60cm mark, each time suspending a load L or the left end and effort E near the right end. Adjust E and or its position so that the rule is balanced. Tabulate the position of L, F and E and the magnitudes of L and E and the distances of load arm
and effort arm. Calculate MA=L/E and VR = effort arm/load arm. It will be found that MA <VR in one case, MA=VR in another and MA>VR in the third case. Try to explain why this is so. Also try to calculate the real load and real effort in these cases.
2. Determine the VR and MA of a given pulley system.
3. Trace the course of different rays of light refracting through a rectangular glass slab at different angles
of incidence, measure the angles of incidence, refraction and emergence. Also measure the lateral
displacement.
4. Determine the focal length of a convex lens by (a) the distant object method and (b) using a needle
and a plane mirror.
5. Determine the focal length of a convex lens by using two pins and formula f = uv/(u+v).
6. For a triangular prism, trace the course of rays passing through it, measure angles i1, i2, A and d. Repeat for
four different angles of incidence (say i1=40° , 50°, 60° and 70°). Verify i1+ i2=A+d and A = r1 + r2 .
7. For a ray of light incident normally (i1=0) on one face of a prism, trace course of the ray. Measure the angle
d. Explain briefly. Do this for prisms with A=60°, 45° and 90°.
8. Calculate the sp. heat of the material of the given calorimeter, from the temperature readings and
masses of cold water, warm water and its mixture taken in the calorimeter.
9. Determination of sp. heat of a metal by method of mixtures.
10. Determination of specific latent heat of ice.
11. Using as simple electric circuit, verify Ohm’s law. Draw a graph, and obtain the slope.
12. Set up model of household wiring including ring main circuit. Study the function of switches and fuses.
Teachers may feel free to alter or add to the above list. The students may perform about 10 experiments.
Some experiments may be demonstrated.
Evaluation
The practical work/project work are to be evaluated by the subject teacher and by an External Examiner.
(The External Examiner may be a teacher nominated by the Head of the school, who could be from the
faculty, but not teaching the subject in the relevant section/class. For example, a teacher of Physics of
Class VIII may be deputed to be an External Examiner for Class X, Physics projects.)
The Internal Examiner and the External Examiner will assess the practical work/project work independently.
Award of marks
• Subject Teacher (Internal Examiner)
• External Examiner
The total marks obtained out of 20 are to be sent to the Council by the Head of the school.
The Head of the school will be responsible for the entry of marks on the mark sheets provided by the
Council.

We hope that every student gets ICSE Class 10 Physics syllabus before starting the preparation for your exam. You can also check ICSE class 10 mathematics syllabus.