Exercise-4A
Question 1. What do you understand by refraction of light?
Solution:
Refraction of light refers to the shift in the direction of the light’s path when it moves from one transparent material to another.
Question 2. Draw diagrams to show the refraction of light from
(i) Air to glass in diagram, label the incident ray, refracted ray, and the angle of incidence (i) and the angle of refraction (r).
(ii) Glass to air. In diagram, label the incident ray, refracted ray, the angle of incidence (i) and the angle of refraction (r).
Solution:
(i) Refraction of light from Air to glass
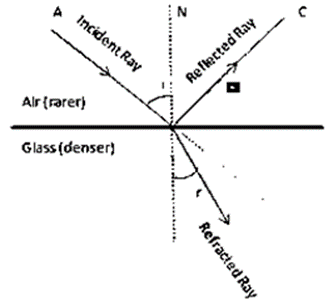
(ii) Refraction of light from Glass to Air

Question 3. A ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction and (ii) the angle of deviation for the ray?
Solution:
The light beam that ordinarily strikes a flat glass slab passes undirected. Because of the ray’s zero degree angle of incidence, it does not bend at the surface. As a result, the angle of refraction r = 0° if the angle of incidence I = 0°. Additionally, the ray’s angle of deviation will likewise be 0°.
Question 4. An obliquely incident light ray bends at the surface due to change in speed, when passing from one medium to other. The ray does not bend when it is incident normally. Will the ray have different speed in the other medium?
Solution:
It will, indeed. The speed of light varies with the medium.
Question 5. What is the cause of refraction of light when it passes from one medium to another?
Solution:
Since light moves through different media at varying speeds, refraction—or a change in the direction of the path of light—occurs. Except for when I = 0°, a light ray’s direction changes as it moves from one medium to another due to a change in speed.
Question 6. A light ray suffers reflection and refraction at the boundary in passing from air to water. Draw a neat labeled ray diagram to show it.
Solution:
While water has a refractive index of 1.33 and is denser than air, air is a more common medium. As a result, as light travels from air to water, it will bend in the direction of normal.
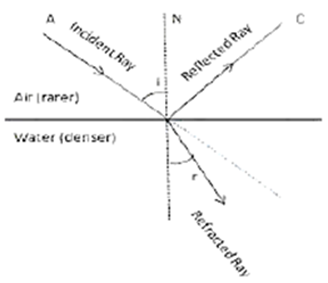
Question 7. A ray of light passes from medium 1 to medium 2. Which of the following quantities of the refracted ray will differ from that of the incident ray: Speed, intensity, frequency, wavelength?
Solution:
Speed, intensity and wavelength
Question 8. State the Snell’s laws of refraction of light.
Solution:
The Snell’s laws of refraction are:
1. The incident ray, the refracted ray, and the normal at the point of incidence all lie in the same plane according to Snell’s rules of refraction.
2. For the given pair of media, the sine of the angle of incidence to the sine of the angle of refraction ratio is constant

where 1μ 2 is referred to as the second media’s refractive index in relation to the first medium.
Question 9. Define the term refraction index of a medium. Can it be less than 1?
Solution:
In relation to a first medium, the refractive index of the second medium is determined by dividing the sine of the angle of incidence in the first medium by the angle sine of the angle of refraction in the second object. Because light always travels at a slower speed in a medium than it does in a vacuum, the refractive index of a media is always larger than 1 (it cannot be less than 1).
Question 10. (i) Compare the speeds of light of wavelength 4000 Å (i.e. violet light) and 8000 Å (i.e. red light) in vacuum.
(ii) How is the refractive index of a medium related to the speed of light in it?
Solution:
(i) Since the medium, not the wavelength, determines the speed of light, the speed will be the same for both.
(ii) A media with a higher refractive index is denser, and as a result, the speed of light in that medium is slower than it would be in a medium with a lower refractive index.
Question 11. A light ray passes from to (a) air, (b) glass. In each case state, how does the speed of light change.
Solution:
Refractive index of water, μw = 1.33
Refractive index of air, μa = 1.0003
Refractive index of glass, μg = 1.5
This implies that μa < μw < μg
When light hits from a rarer to a denser medium, its speed reduces, and when it enters from the denser to a rarer media, it rises. The speed of light therefore rises when a light ray travels from water to air and decreases when a light beam travels from water to glass.
Question 12. A light ray in passing from water to a medium
(a) Speeds up
(b) Slows down. In each case, give one example of the medium.
Solution:
(a) A speed increase indicates that the medium’s refractive index is lower than that of water.
(b)When the speed slows, it indicates that the medium has a higher refractive index than water.
Question 13. What do you understand by the statement the refractive index of glass is 1.5 for white light?
Solution:
White light travels through air 1.5 times more quickly than in glass due to the refractive index of glass, which is 1.5 for white light.
Question 14. A monochromatic ray of light passes from air to glass the wavelength of light in air is λ, the speed of light in air is c and in glass is ν. If the absolute refractive index of glass is 1.5, write down
(a) The relationship between 𝒸 and ν,
(b) The wavelength of light in glass.
Solution:
(a) The formula for the relationship between the speed of light in glass and air is provided by
𝑐𝑣= 𝜇 o𝑟 𝑐=1.5
(b) The wavelength of light in glass (λ 1)

Question 15. In an experiment of finding the refractive index of glass, if blue light is replaced by the red light, how will the refractive index of glass change? Give reason in support of your answer.
Solution:
Blue light travels through glass at a slower speed than red light. The refractive index is now μ=c/v. As a result, glass will have a lower refractive index for red light than for blue light.
Question 16. (i) For which color of white light, is the refractive index of a transparent medium
(a) the least
(b) the most?
(ii) Which color of light travels fastest in any medium except air?
Solution:
(i) For which color of white light, is the refractive index of a transparent medium
(a) the least – red color
(b) the most – violet color
(ii) Red color has the highest wavelength, thus it moves at the quickest speed.
Question 17. Name two factors on which the refractive index of a medium depends? State how it depends on the factors stated by you.
Solution:
The two elements that determine a medium’s refractive index are:
1) A medium’s physical characteristics, such as its optical density (e.g., g = 1.5, w = 1.33) – A medium’s refractive index increases when the speed of light decreases in that medium compared to air.
2) Physical factors like temperature – when the temperature rises, the speed of light in the medium also increases, resulting in a drop in the medium’s refractive index.
Question 18. How does the refractive index of a medium depend on the wavelength of light used?
Solution:
As the wavelength of light increases, a medium’s refractive index drops.
A medium’s refractive index is higher for violet light (light with the shortest wavelength) than for red light (greatest wavelength).
Question 19. How does the refractive index of a medium depend on its temperature?
Solution:
A medium’s refractive index falls as temperature rises.
The refractive index (= velocity of light in vacuum/velocity of light in medium) drops when temperature rises because the speed of light in that medium increases.
Question 20. Light of a single color is passed through a liquid having a piece of glass suspended in it. On changing the temperature of liquid, at a particular temperature the glass piece is not seen.
(i) When is the glass piece not seen?
(ii) Why is the light of a single color used ?
Solution:
(i) The glass piece cannot be seen when the refractive indices of liquid and glass are equal.
(ii) Light of a single hue is employed because different colors of light behave differently depending on the refractive index of the medium (glass or liquid).
Question 21. A ray of light from air suffers partial reflection and refraction at the boundary of water.

Complete the diagram showing (i) the reflected ray B and (ii) the refracted ray C.
How are the angles of incidence i and refraction r related?
Solution:

Snell’s law establishes a relationship between the angles of incidence and refraction

Question 22. The diagram alongside shows the refraction of a ray of light from sir to a liquid
(a) Write the values of
(i) angle of incidence,
(ii) angle of refraction.
(b) Use Snell’s law to find the refractive index of liquid with respect to air.
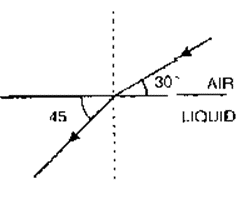
Solution:
(a)
(i) The angle that the incident ray creates with the normal is known as the angle of incidence
∠I = 90° – 30°
∠I = 60°
(ii) The angle that the refracted beam creates with the normal is known as the angle of refraction.
∠I = 90° + 45°
∠I = 45°
(b) According to Snell’s law

Question 23. The refractive index of water with respect to air is a μ w and of glass with respect to air is a μ g. Express the refractive index of glass with respect to water.
Solution:
Glass’s refractive index in relation to water wμ g is given by

Question 24. What is lateral displacement? Draw a ray diagram showing the lateral displacement of a ray of light when it passes through a parallel sided glass slab.
Solution:
The term “lateral displacement” refers to the angle formed between the emerging ray’s route and the incident ray’s direction. XY in the image above represents the lateral displacement or perpendicular distance.
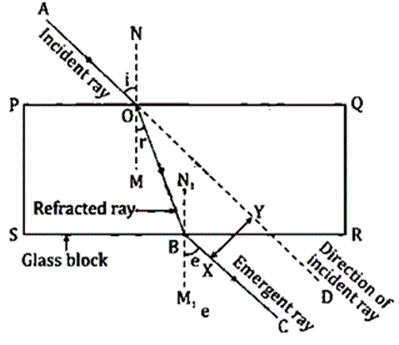
Question 25. (i) A ray of light strikes the surface of a rectangular glass block such that the angle of incidence in air is 0°.In each case, draw diagram to show the path taken by the ray as it passes through the glass block and emerges from it.
(ii) A ray of light strikes the surface at a rectangular glass slab such that the angle of incidence is 45o.
In each case, draw diagram to show the path taken by the ray as it passes through the glass slab and emerges from it.
Solution:
(i) When angle of incidence is 0°
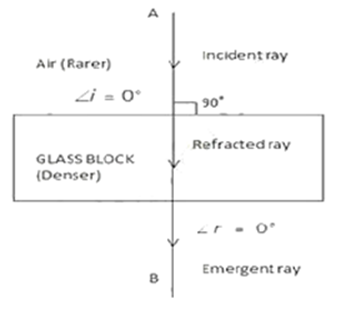
(ii) When angle of incidence is 45°.

Question 26. In the adjacent diagram, AO is a ray of light incident on a rectangular glass block.
(a) Complete the path of the ray till it emerges out of the block.
(b) In the diagram, mark the angles of incidence (i) and the angle of refractive index of glass related to the angles 𝔦 and 𝔯?
(c) Mark angles of emergence by the letter ℯ. How are the angles I and e related?
(d) Which two rays are parallel to each other? Name them.
(e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray.
Solution:
(a) The complete path of incident ray in glass block is drawn in figure below.

(b) The angles of incidence (i) and refraction (r) are partially noted (a).
Glass’s refractive index (μ) and angles are connected as follows:

(c) The two angles are connected to one another by the relationship I = e in and (d) the incident ray and emerging ray are parallel to one another.
(e) The lateral displacement in the figure is denoted by XY.
Question 27. A ray of monochromatic green light enters a liquid from air, as shown in Fig 4.20. The angle 1 is 45° and angle 2 is 30°.
(a) Find the refractive index of liquid.
(b) Show in the diagram the path of the ray after it strikes the mirror and re-enters in air. Mark in the diagram the angles where ever necessary.
(c) Redraw the diagram if plane mirror becomes normal to the refracted ray inside the liquid. State the principal used.
Solution:
(a) Refractive index of the liquid =


Question 28. When an illuminated object is held in front of a thick plane glass mirror, several images are seen, out of which the second image is the brightest. Give reason.
Solution:
Nearly 4 percent of the light that strikes the surface of a thick plane glass mirror is reflected, creating the first picture, which is a weak virtual image, while nearly 96 percent of the light is refracted inside the glass. The glass’s silvered surface is now brightly reflecting this beam back. A second virtual picture is created when this beam is partially refracted in air. Because of the light’s intense reflection off of the silver surface, this image is the brightest.
Question 29. Fill in the blanks to complete the following sentences:
(i) When light travels from a rarer to a denser medium, its speed ……………..
(ii) When light travels from a denser to a rarer medium, its speed ……………….
(iii) The refractive index of glass with respect to air is 3/2. The refractive index of air with respect to glass will be ……………….
Solution:
(i) When light travels from a rarer to a denser medium, its speed decreases.
(ii) When light travels from a denser to a rarer medium, its speed Increases.
(iii) The refractive index of glass with respect to air is 3/2. The refractive index of air with respect to glass will be 2/3 .
Exercise-4A
Multiple Choice Types
Question 1. When a ray of light from air enters a denser medium, it:
a) Bends away from the normal
b) Bends towards the normal
c) Goes un-deviated
d) Is reflected back
Solution: b) bends towards the normal.
Question 2. A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incident is:
a) 0°
b) 45°
c) 60°
d) 90°
Solution: a) 0°
Question 3. The highest refractive index is of:
a) Glass
b) Water
c) Diamond
d) Ruby
Solution: c) Diamond
Exercise-4A
Numericals
Question 1. The speed of light in air is 3 × 108 ms-1. Calculate the speed of light in glass. The refractive index of glass is 1.5.
Solution:
It is given that,
Speed of light in air, c = 3 × 108 m/s
Refractive index of glass, μ = 1.5
Speed of light in glass, v = ?
We know that,

Question 2. The speed of light in diamonds is 125,000 km s-1. What is its refractive index? (speed of light in air = 3 × 108 ms-1).
Solution:
It is given that,
Speed of light in diamond, v = 125 × 106 m/s
Speed of light in air, c = 3 × 108 m/s
Refractive index of diamond, μ D = ?
We know that,
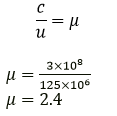
Question 3. The refractive index of water with respect to air is 4/3. What is the refractive index of air with respect to water?
Solution:
It is given that,
Refractive index of water w.r.t. air
Air µ water =4/3
Refractive index of air w.r.t. water is:

Question 4. A ray of light of wavelength 5400 Å suffers refraction from air to glass. Taking αμℊ = 3/2, find the wavelength of light in glass.
Solution:
It is given that, refractive index of glass w.r.t. air

Exercise-4B
One Line Answer
Question 1. What is a prism? With the help of diagram of a prism, indicate its refracting surfaces, refracting edge and base.
Solution:
A prism is a transparent refracting medium bounded by five plane surfaces inclined at some angle.

Question 2. The following diagrams (a) and (b) in Fig. 4.29 below show the refraction of a monochromatic ray of light through a parallel sided glass block and a prism respectively.
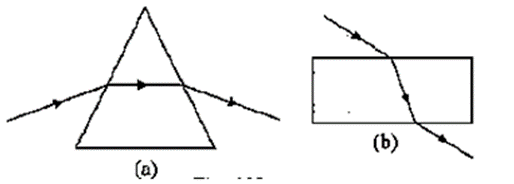
(a) In each diagram, label the incident, refracted, emergent rays and the angle of deviation. (b) In what way the direction of emergent ray in the two cases differ with respect to the incident ray? Explain your answer.
Solution:
(a)

(b) The emerging ray for the prism is not parallel to the incident ray, but it is for the glass block. This is due to the fact that refraction occurs at two inclined surfaces in a prism but at two parallel surfaces in a glass block
Question 3. Define the term angle of deviation
Solution:
The angle of deviation is the angle formed by the incident and emerging ray directions.
Question 4. Complete the following sentence:
Angle of deviation is the angle which the …………………. Ray makes with the direction of ………………….. ray.
Solution:
Angle of deviation is the angle which the emergent ray makes with the direction of incident ray.
Question 5. What do you understand by the deviation produced by a prism? Why is it caused? State three factors on which the angle of deviation depends.
Solution:
The light beam is refracted at two sides of a prism. Both the first surface and the second surface of the prism exhibit deviations. So, a prism causes the path of light to diverge. The angle of deviation (or deviation a prism produces) is determined by the angles of incidence I the material of the prism (i.e., the refractive index), the prism’s angle (A), and the color or wavelength (λ) of the light being used.
Question 6.(i) How does the angle of deviation produced by a prism change with increase in the angle of incidence. Draw a curve showing the variation in the angle of deviation with the angle of incidence at a prism surface.
(ii) Using the curve in part (a) above, how do you infer that for given prism, the angle of minimum deviation δmin is unique for the given light.
Solution:
(i) The angle of deviation initially reduces as the angle of incidence increases, reaching a minimum value (m) for a certain angle of incidence. The angle of deviation is seen to grow as the angle of incidence is increased further.
Angle of deviation () and angle of incidence (i) variations:
(ii) The angle of minimal deviation is unique for a given prism and colour of light because only one horizontal line can be drawn at the lowest point of the i- curve that is parallel to the i-axis.
Question 7. State whether the following statement is ‘true’ or ‘false’.
The deviation produced by a prism is independent of the angle of incidence and is same for all the colors’ of light
1. True
2. False
Solution: False.
Question 8. How does the deviation produced by a prism depend on the
(i) Refraction index of its material
(ii) Wavelength of incident light
Solution:
(i) A prism with a higher refractive index than a prism with a lower refractive index creates a larger deviation for a given angle of incidence.
(ii) For light of different colours, a medium’s refractive index varies. It gets bigger as the wavelength gets smaller. As a result, violet light has the highest refractive index while red light has the lowest. As a result, the prism deviates red light the least and violet light the most, or i.e., δviolet > δred
Question 9. How the angle of minimum deviation does produces by a prism change with increase in
(i) The wavelength of incident light
(ii) The refracting angle of prism
Solution:
(i) Angle of deviation changes as incident light wavelength increases; as wavelength increases, angle of deviation decreases.
(ii) The prism’s refracting angle. With an increase in prism angle, the angle of deviation also rises.
Question 10. Write a relation for the angle of deviation (δ) for a ray of light passing through an equilateral prism in terms of the angle of incidence (i) angle of emergence (ℯ) and angle of prism (A).
Solution:
For a light beam travelling through an equilateral prism, the relationship between the angle of incidence (I) angle of emergence (e), angle of prism (A), and angle of deviation (δ) is
δ = (i+e) – A
Question 11. A ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2.
(i) How is the angle of emergence ‘i2’ related to the angle of incidence ‘i2’?
(ii) What can you say about the angle of deviation in such a situation?
Solution:
(i) i2 = i1
(ii) Angle of deviation is minimum explanation, if the prism is equilateral and the angle of incidence equals the angle of emergence, the refracted ray inside the prism moves parallel to it at the smallest deviation position.
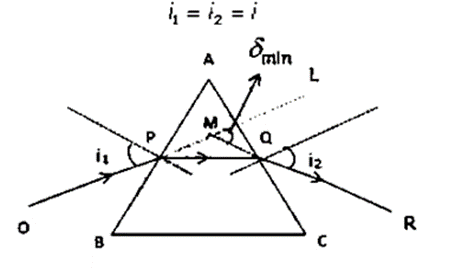
Question 12. Draw a ray diagram to show the refraction of a monochromatic ray through a prism when it suffers minimum deviation. How is the angle of emergence related to the angle of incidence in this position?
Solution:
When an equilateral prism is in the minimal deviation position δ = δmin, the angle of incidence i1 and the angle of emergence i2 are identical.
Question 13. A light ray of yellow color is incident on an equilateral glass prism at an angel of incidence equal to 48° and suffers minimum deviation by an angle of 36°.
(i) What will be the angle of emergence?
(ii) If the angle of incidence is changes to
(a) 30°, (b) 60°, State whether the angle of deviation will be equal to, less than or more than 36° ?
Solution:
(i) As the ray is suffering minimum deviation in an equilateral glass prism so, 𝔦1 = 𝔦2, 𝔦2 = 48°
(ii) If the angle of incidence is changed to
(a) If the angle of incidence is changed to 30° the angle of deviation will be more than 36°
(b) If the angle of incidence is changed to 60°, the angle of deviation will be more than 36°.
Question 14. Name the color of white light which is deviated
(i) The most,
(ii) The least, on passing through a prism.
Solution:
(i) the most – Violet color
(ii) The least – Red color
Question 15. Which of the two prisms, A made of crown glass and B made of flint glass, deviate a ray of light more?
Solution:
B constructed of glass flint. As a result of its increased refractive index
Question 16. How does the angle of deviation depend on the refracting angle of the prism?
Solution:
With an increase in prism angle, the angle of deviation (δ) rises (A)
Question 17. An object is viewed through a glass prism with its vertex pointing upwards. It appears to be displaced upward. Explain the reason.
Solution:
Let’s say that the prism is struck by the two rays OA and OL from the source O. From the prism’s front face, they are refracted along the AB and LM axes. These two rays once more refract off the prism’s second face and exit along BC and MN, respectively, giving the impression that they are coming from I.

Question 18. A ray of light is normally incident on one face of an equilateral glass prism. Answer the following:
i) What is the angle of incidence on the first face of the prism?
ii) What is the angle of refraction from the first face of the prism?
iii) What will be the angle of incidence at the second face of the prism?
iv) Will the light ray suffer minimum deviation by the prism?
Solution:
i) The angle of incidence is 0° if the incident ray is normal to the prism.
ii) Here, the angle of refraction from the first face, r1, is equal to zero degrees.
iii) A = 60° and r1 = 0° since the prism is equilateral. Therefore, the angle of incidence at the prism’s second face will be 60°.
iv) No, The light won’t experience the small deviation.
Question 19. In following figure shows two identical prisms A and B placed with their faces parallel to each other A ray of light of single color PQ is incident at the face of the prism A. complete the diagram to show the path of the ray till it emerges out of the prism B.

Solution:

Exercise-4B
Multiple Choice Types
Question 1. In refraction of light through a prism, the light ray:
a) Suffers refraction only at one face of the prism
b) Emerges out from the prism in a direction parallel to the incident ray
c) Bends at both the surfaces of prism towards its base
d) Bends at both the surfaces of prism opposite to its base.
Solution: c) Bends at both the surfaces of prism towards its base.
Question 2. A ray of light suffers refraction through an equilateral prism. The deviation produced by the prism does not depend on the:
a) Angle of incidence
b) Color of light
c) Material of prism
d) Size of prism
Solution: d) size of prism.
Question 1. A ray of light incident at an angle 48o on a prism of refracting angle 60o suffers minimum deviation. Calculate the angle of minimum deviation. [Hint: δmin = 2i – A]
Solution:
It is given that,
Angle of incidence, i = 48°
Refracting angle, A = 60°
Angle of minimum deviation,
δmin = ?
δmin = 2i – A
δmin = 2(48) – 60
δmin = 36°
Question 2. What should be the angle of incidence for a ray of light which suffers a minimum deviation of 36o through an equilateral prism?
[Hint: A = 60°, i = (A + δmin)/2]
Solution:
It is given that,
Angle of prism, A = 60°
Angle of minimum deviation, δmin = 36°
Angle of incidence, I = ?
As δmin = 2i – A
36° = 2i- 60
i = 48°
Exercise-4C
One Word Type
Question 1. How is the refractive index of a medium related to the real and apparent depths of an object in that medium?
Solution:
Relationship between refractive index and real and apparent depths

Question 2. Prove that
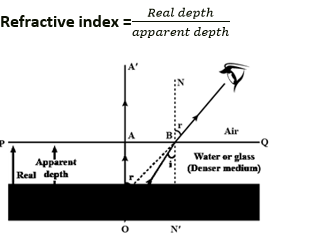
Solution:
A light beam that is incident regularly along OA. It travels directly along OAA’. Take into account a second ray that is incident along OB at an angle I from O (the object). This ray is bent and propagates along BC. Since this beam BC seems to originate from point I when it is produced backward, AI denotes the apparent depth, which is smaller than the actual depth AO.
Since AO and BNI are parallel and OB is the transversal
∠ AOB = ∠OBNI (Alternate angles)
∠BIAI = ∠CBN (Corresponding angles)

Question 3. A postage stamp kept below a rectangular glass block of refractive index 1.5 when viewed from vertically above it, appears to be raised by 7.0 mm. calculate the thickness of the glass block.
Solution:
Refractive index of the glass block, 𝛍g = 1.5 Shift in the image = 7mm or 0.7 cm
Thickness of glass block or real depth =?
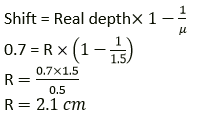
Exercise-4D
Question 1. Explain the term critical angle with the aid of a labeled diagram.
Solution:
Critical angle: The critical angle is the angle of incidence in the denser media at which the angle of refraction in the rarer medium is 90°.

Question 2. How is the critical angle related to the refractive index of a medium?
Solution:
The relationship between the critical angle and a medium’s refractive index

Question 3. State the approximate value of the critical angle for
(i) glass-air surface
(ii) Water-air surface.
Solution:
(i) For a glass-air surface, the critical angle is

Question 4. What is meant by the statement the critical angle for diamond is 24°?
Solution:
Diamond’s critical angle is 24°. This suggests that the angle of refraction in the air will be 90° at an incidence angle of 24° within the diamond. Furthermore, if the incidence angle exceeds this angle, the beam will experience entire internal reflection without any refraction.
Question 5. A light ray is incident from a denser medium on the boundary separating it from a rarer medium an angle of incident equal to the critical angle, what is the angle of refraction for the ray?
Solution:
The angle of refraction changes to 90° when a ray is incident from a denser media to a rarer medium at an angle equal to the critical angle (i=ic).
Question 6. Name two factors which affect the critical angle for a given pair of media. State how the factors affect it.
Solution:
The factors which affect the critical angle are:
(i) The color (or wavelength) of light and
(ii) Temperature has two variables that have an impact on the critical angle.
(iii)The impact of light color: The critical angle for a pair of media is different for red and violet light. Thus, the crucial angle grows as light’s wavelength rises.
(iv) Effect of temperature: The critical angle rises as the temperature rises because the medium’s refractive index falls as the temperature rises.
Question 7. The critical angle for glass-air is 45° for the light of yellow color. State whether it will be less than, equal to, or more than 45° for
(i) Red light
(ii) Blue light?
Solution:
Refractive index increases (or lowers) with wavelength, whereas critical angle reduces (or increases) (or more)
(i) For red light the critical angle will be more than -45°
(ii) For blue light the critical angle will be less than -45°.
Question 8. (i) What is total internal reflection?
(ii) State two conditions necessary for total internal reflection to occur.
(iii) Draw diagram to illustrate the total internal reflection
Solution:
(i) This phenomena occurs when a light beam travelling through a denser medium is incident at the surface of a rarer medium at an angle larger than the pair’s critical angle, completely reflecting back into the denser medium.
(ii) The two necessary conditions for total internal reflection are:
(a) The light must go from a denser to a rarer medium.
(b)The incidence angle needs to be larger than the critical angle for the two media.
(iii) In the event of entire internal reflection, or when the incidence angle exceeds the critical angle.
Question 9. (i) Fill in the blanks to complete the following sentence:
Total internal reflection occurs only when a ray of light passes from a …………….. Medium to a ………………. Medium.
(ii) Critical angle is the angle of ……………. In denser medium for which the angle of ………….. in the rarer medium is………………….
Solution:
(i) Total internal reflection occurs when a ray of light passes from a denser medium to a rarer medium.
(ii) Critical angle is the angle of incidence in denser medium for which the angle of refraction in rarer medium is 90°.
Question 10. State whether the following statement is true or false:
If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium.
a) True
b) False
Solution: True
Question 11. The refractive index of air with respect to glass is expressed as Gμa= sinsin i/sinsin r
(a) Write down a similar expression for aμg in terms of the angles i and r.
(b) If angle r = 90°, what is the corresponding angle i called?
(c) What is the physical significance of the angle i in part (b)?
Solution:
(a) aμg = sin𝑟sin
(b) If the refractive angle, r, is 90 degrees, the corresponding incidence angle, I will also be 90 degrees, or the critical angle.
(c) Total internal reflection will happen if the angle of incidence is greater than the value of I calculated in section (b) (i.e., the critical angle).
Question 12. In following figure, show two rays A and B travelling from water to air. If the critical angle for water- air surface is 48°, complete the ray diagram showing the refracted rays for each. State conditions when the ray will suffer total internal reflection.

Solution:
The necessary conditions for the total internal reflection to occur are
(i) For light to go from a denser medium to a rarer one, both must be denser.
(ii) The incidence angle must be larger than the critical angle the incidence angle in this instance. ∠I>48°

Question 13. The given figure shows a point source P inside a water container three rays A, B, and C starting from the source P are shown up to the water surface.
(a) Show in the diagram the path of these rays after striking the water. The critical angle for water-air surface is 48°.
(b) Name the phenomenon which the rays A, B, and C exhibit.

Solution:
(a)

(b) The “refraction of light” phenomena may be seen in Rays A and B.
The occurrence of “complete internal reflection” is shown in Rays C.
Question 14. In the given figure PQ and PR are the two light rays emerging from an object P. The ray PQ is refracted as QS.

(a) State the special name given to the angle of incidence ∠PQN of the ray PQ.
(b) What is the angle of refraction for the refracted ray QS?
(c) Name the phenomenon that occurs if the angle of incidence ∠PQN is increased.
(d) The ray PR suffers partial reflection and refraction on the water-air surface. Give reason. Draw in the diagram the refracted ray for the incident ray PR and hence show the position of image of the object P by the letter P’ when seen vertically from above.
Solution:
(a) Critical angle:- Critical angle is the angle of incidence in the denser media for which the angle of refraction in the rarer medium is 90°.
(b) 90°
(c) Total internal reflection:- Total internal reflection, when the light beam is reflected back into the same medium instead of being refracted, happens when the angle of incidence is larger than the critical angle.
(d) The angle of incidence for the ray PR is smaller than the critical angle (i.e., PQS), which causes partial reflection and refraction at the interface of two media according to the rules of reflection.

Question 15. The refractive index of glass is 1.5. From a point P inside a glass block, draw rays PA, PB and PC incident on the glass air surface at an angle of incidence 30°, 42° and 60° respectively.
(a) In the diagram show the approximate direction of these rays as they emerge out of the block.
(b) What is the angle of refraction for the ray PB?
(Take sin 42°=2/3)
Solution:
(a)
μ = 1.5

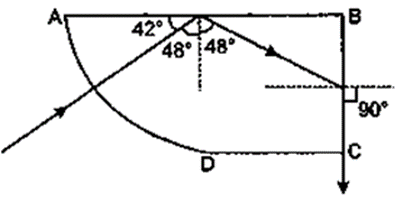
Question 16. A ray of light enters a glass slab ABDC as shown in fig. 4.59 and strikes at the centre O of the circular part AC of the slab. The critical angle of glass is 42°. Complete the path of the ray till it emerges out from the slab. Mark the angles in the diagram wherever necessary.
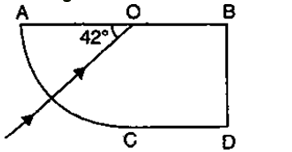
Solution:
The illustration below shows the finished ray diagram.
Question 17. What is a total reflecting prism? State three actions that it can produce. Draw a diagram to show one action of the total reflecting prism.
Solution:
A whole reflecting prism is one with a 90° angle between its two refracting surfaces and two additional angles of 45° each. Normal light that strikes one of its faces experiences complete internal reflection inside the prism.
Due to this behavior, a total reflecting prism is used to produce following three actions:
(a) In order to deviate a light beam through 90 degrees.
(b) Deviate a light ray through 180 degrees, and
(c) Construct the inverted picture without creating a deviation in its course.
In order to raise the inverted picture without causing a divergence in its course, an erecting prism is utilized.

Question 18. Show with the help of a diagram how a total reflecting prism can be used to turn a ray of light through 90°. Name one instrument in which such a prism is used.
Solution:
As seen in the diagram, a light beam contacts the prism’s face AB regularly, travelling un-deviated to face AC, where it forms a 45° angle with respect to AC. Rays suffer from entire internal reflection and reflect at a 45° angle because the incidence angle in this situation is greater than the critical angle. When the beam reaches face BC, it is incident properly and passes through without deviating. The incident beam is afterwards 90° diverted. A periscope uses a prism of this type.

Question 19. A ray of light OP passes through a right angles prism as shown in the adjacent diagram.
(a) State the angles of incidence at the faces AC and BC.
(b) Name the phenomenon which the ray suffers at the face AC.

Solution:
(a) The angle of incidence at face AC is 45 degrees, whereas the angle at face BC is 0 degrees.
(b) At the face AC, the beam experiences complete internal reflection.
Question 20. In following figure, a ray of light PA is incident normally on the hypotenuse of an isosceles right angle prism ABC. (a) Complete the path of the ray PQ till it emerges from the prism. Mark in the diagram the angle wherever necessary. (b) what is the angle of deviation of the ray PQ? (c) Name a device in which this action is used.

Solution:
(a)

(b) Angle of deviation = 180°
(c) Prism binocular
Question 21. In given figure a ray of light PQ is incident normally on the face AB of an equilateral glass prism. Complete the ray diagram showing its emergence into air after passing through the prism.
(a) Write the angles of incidence at the faces AB and AC of the prism.
(b) Name the phenomenon which the ray of light suffers at the face AB, AC and BC of the prism.

Solution:
(a) At the face AB, i=0° and at the face AC, i= 60°
(b) At the face AB – refraction,
At the face AB – total internal reflection,
At the face BC – refraction

Question 22. Draw a neat labeled ray diagram to show the total internal reflection of a ray of light normally incident on one face of a 30°, 90°, 60° prism.
Solution:
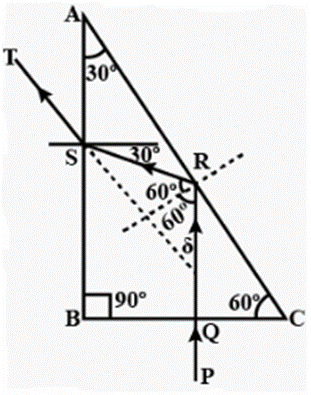
Question 23. Two isosceles right –angles glass prisms are placed near each other as shown in Fig. 4.63. Complete the path of the light ray entering the first prism till it emerges out of the second prism.
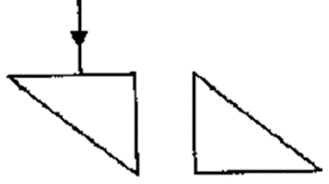
Solution:

Question 24. What device other than a plane mirror can be used to turn a ray of light through 180°? Draw a diagram in support of your answer. Name an instrument in which this device is used.
Solution:
A light ray may be rotated 180 degrees by using a whole reflection prism. The diagram that follows can help to clarify it further. Binoculars use a prism to achieve this effect.

Question 25. Mention one difference between reflection of light from a plane mirror and total internal reflection of light from a prism.
Solution:
When a prism produces complete internal reflection, the full amount of incoming light (100%) is reflected back into the denser medium. While in a typical reflection from a flat mirror, some light is refracted and absorbed, resulting in a partial reflection.
Question 26. State one advantage of using a total reflecting prism as a reflector in place of plane mirror
Solution:
We get a significantly brighter image utilizing a fully reflecting prism than we would have with a flat mirror.
Exercise-4D
Multiple Choice Types
Question 1. The critical angle for glass-air interface is :
a) 24°
b) 48°
c) 42°
d) 45°
Solution: 42°
Question 2. A total reflecting right angled isosceles prism can be used to deviate a ray of light through
a) 30°
b) 60°
c) 75°
d) 90°
Solution: d) 90°
Question 3. A total reflecting equilateral prism can be used to deviate a ray of light through:
a) 30°
b) 60°
c) 75°
d) 90°
Solution: b) 60°




