Selina ICSE Class 10 Physics Solutions Chapter 8 Current Electricity

EXERCISE-8A

Question 1. Define the term current and state its S.I unit.
Solution:
The speed at which charges flow is known as current.
I=q/t

Question 2. Define the term electric potential. State its S.I. unit.
Solution:
Potential at a point is the effort put in to move a unit positive charge there from infinity. Volt is a SI unit, with 1 V equaling 1 joule/1 coulomb.

Question 3. How is the electric potential difference between the two points defined? State its S.I. unit.
Solution:
The effort required to move a unit positive charge from one location to the other is equal to the potential difference between two points.
Volt is its SI unit.

Question 4. Explain the statement ‘the potential difference between two points is 1 volt’.
Solution:
When one joule of work is done to transport a charge of one coulomb from one place to another in an electric circuit, the potential difference between the two locations is measured in volts.

Question 5. State whether the current is a scalar or vector?
(i) What does the direction of current convey?
(ii) What does the positive and negative sign of potential convey?
Solution:
(i) A scalar quantity, current. The flow of electrons is opposed to the flow of current, as shown by the direction of the current.
(ii) A scalar quantity is also potential. The positive sign of potential indicates that, because of the positive charge that was used to get it from infinity, effort must be done to oppose the repellent force on the positive test charge. The potential’s negative sign indicates that the attracting force is at work on the negative test charge.

Question 6. (i) Name the particles which are responsible for the flow of current in a metallic wire.
(ii) Explain the flow of current in a metallic wire on the basis of movement of the particles named by you above in part.
(iii) What is the cause of resistance offered by the metallic wire in the flow of current through it?
Solution:
(i) Free electrons are the particles that cause the current to flow across a metallic wire.
(ii) The moving charges that cause electricity to conduct in metals are free electrons. If n electrons flow through a metallic conductor in time t, then Q (charge) = n x e is the total charge that has flown (charge on an electron).
(iii) Free electrons and fixed positive ions both exist in metal. Positive ions acquire a positive charge by giving up their valence electrons. When a potential difference is provided across the circuit and free electrons start to move, they collide with these fixed positive ions since electrons are free for movement but positive ions are not. The metallic wire’s main source of resistance to current passage through it is this collision.

Question 7. State Ohm’s law and draw a neat labeled circuit diagram containing a battery, a key, a voltmeter, an ammeter, a rheostat and an unknown resistance to verify it.
Solution:
Free electrons and fixed positive ions both exist in a metal. Positive ions acquire a positive charge by giving up their valence electrons. When a potential difference is provided across the circuit and free electrons start to move, they collide with these fixed positive ions since electrons are free for movement but positive ions are not. The metallic wire’s main source of resistance to current passage through it is this collision.

Question 8.State Ohm’s law and draw a neat labeled circuit diagram containing a battery, a key, a voltmeter, an ammeter, a rheostat, and an unknown resistance to verify it.
Solution:
According to this, if the temperature of a metallic wire is constant, the amount of electric current flowing through it is exactly proportional to the potential difference V at its ends. Ohm’s law is the name for this.
V = IR

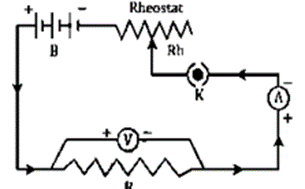
Question 9. (a) Name and state the law which relates the potential difference and current in a conductor.
(b) What is the necessary condition for a conductor to obey the law named above in part (a)?
Solution:
(a) Ohm’s law is the name of the rule. It claims that, if the temperature is constant, the current flowing through a conductor is directly proportional to the potential difference across its ends.
(b) The temperature ought to be constant.

Question 10. (a) Draw a V-I graph for a conductor obeying Ohm’s law.
(b) What does the slope of V–I graph for a conductor represent?
Solution:
(a)

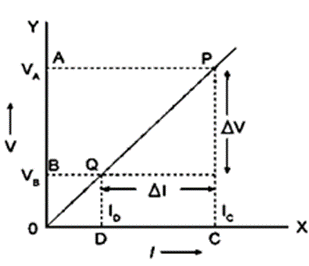
(b) The resistance constant is depicted by the VI graph’s slope..

Question 11. Draw a I – V graph for a linear resistor. What does its slope represent?
Solution:

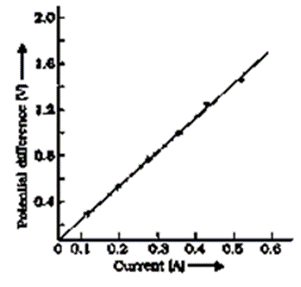
Question 12. What is an ohmic resistor? Give one example of an ohmic resistor. Draw a graph to show its current voltage relationship. How is the resistance of the resistor determined from this graph?
Solution:
Ohmic Resistor: A resistor that upholds by Ohm’s law is an ohmic resistor. As an illustration, all metallic conductors (such as silver, aluminum, copper, iron etc.)

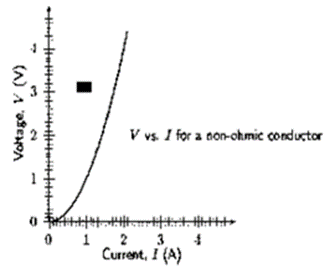
Question 13. What are non-ohmic reistors? Give one example and draw a graph to show its current-voltage relationship.
Solution:
Non-ohmic resistors are conductors that do not adhere to Ohm’s Law. As in a diode valve.

Question 14. Give two differences between an ohmic and non-ohmic resistor.
Solution:
(1) Non-ohmic resistors do not adhere to Ohm’s Law, which states that V/I is not the same for all values of V or I. Ohmic resistors, on the other hand, adhere to Ohm’s Law.
(2) The V-I graph in an ohmic resistor is linear, but the V-I graph in a non-ohmic resistor is non-linear.

Question 15. Figure, below shows the I-V characteristic curves for four resistors Identify the ohmic and non-ohmic resistors. Give a reason for your answer.

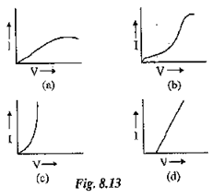
Solution:
Ohmic: (d),
Non-Ohmic: (a),(b)and(c)
Only for (d) the I-V graph is a straight line or linear while for (a), (b) and (c), the graph is a curve.

Question 16. Draw a V-I graph for a conductor at two different temperatures. What conclusion do you draw from your graph for the variation of resistance of conductor with temperature?
Solution:

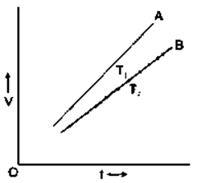
T1 exceeds T2 in the graph above. Given that line B is less steep than line A, we may infer that conductor resistance is higher at high temperature T1 than at low temperature T2. As a result, we may state that a conductor’s resistance rises as temperature rises.

Question 17. (i) How does the resistance of a wire depend on its radius? Explain your answer.
(ii) Two copper wires are of the same length, but one is thicker than the other.
(1) Which wire will have more resistance?
(2) Which wire will have more specific resistance?
Solution:
(i) The resistance of a wire is inversely related to its cross-sectional area..

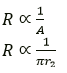
This indicates that a wire of the same length but with a twofold radius has a resistance of one-fourth.
(ii) A wire’s resistance is directly proportional to its length (l) and inversely proportionate to its cross-sectional area

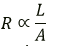
Since resistance is inversely related to cross-sectional area, thinner wires have higher resistance.
1. Resistivity or specific resistance is p = RA/l
2. As a result, the thicker wire will have greater specific resistance since resistivity is inversely correlated with cross-sectional area.

Question 18. How does the resistance of a wire depend on its length? Give a reason for your answer with reason.
Solution:
A wire’s resistance is inversely correlated with its length.
R ∝ I
The amount of collisions an electrical conductor experiences as electrons go from one end to the other is what determines how resistant the conductor is. Obviously, a longer conductor will experience more collisions than a shorter conductor. A longer conductor hence provides higher resistance.

Question 19. How does the resistance of a metallic wire depend on its temperature? Explain with reason.
Solution:
Both the amplitude of vibration of fixed positive ions and the random mobility of electrons increase with the conductor’s temperature. As a result, there are more collisions. As a result, a conductor’s resistance rises as its temperature climbs. When a bulb is shining (i.e., when it is at a high temperature), as opposed to when it is not glowing, the filament’s resistance is higher (i.e., when it is cold).

Question 20. Two wires one of copper and other of iron, are of the same length and same radius. Which will have more resistance? Give reason.
Solution:
Due to iron’s higher resistivity than copper’s, iron wire of the same length and radius will exhibit more resistance.

Question 21. Name three factors on which resistance of a given wire depends and state how is it affected by the factors stated by you.
Solution:
(i) A wire’s resistance is directly inversely proportional to its length, meaning that as length grows, resistance likewise rises. R ∝ I
(ii) A wire’s resistance is inversely correlated with its cross-sectional area. Resistance will be lower if the wire’s cross-sectional area is larger, and vice versa. R > 1
(iii) Because more collisions occur at higher temperatures, resistance rises as a function of temperature.
(iv) Resistance varies with conductor type because the concentration of free electrons in various materials varies. Silver, copper, and other materials offer less resistance and are referred to as good conductors, whereas rubber, glass, and other materials offer extremely high resistance and are referred to as insulators.

Question 22. Define the term resistivity and state its S.I unit.
Solution:
A material’s resistance is measured by the resistance of a wire made of that material with the same cross-sectional area and length. Ohm metre is a SI unit.

Question 23. Write an expression connecting the resistance and resistivity. State the meaning of symbols used.
Solution:
We can write it as,
R=ρ (I/A)
Here,
ρ – resistivity
R – resistance
l – length of conductor
A – area of cross-C-section

Question 24. State the order of resistivity of (i) a metal, (ii) a semiconductor and (iii) an insulator.
Solution:
Metal < Semiconductor < Insulator

Question 25. (i) Name two factors on which the specific resistance of a wire depends?
(ii) Two wires A and B are made of copper. The wire A is long and thin while the wire B is Short and thick. Which will have more specific
resistance?
Solution:
(i) A wire’s particular resistance is influenced by the substance’s temperature and material.
(ii) The wire’s substance determines the specific resistance, not its size. Consequently, the specific resistance of both wires will be the same.

Question 26. Name a substance of which the resistance remains almost unchanged by the increase in temperature.
Solution:
A substance of which the resistance remains almost unchanged by the increase in temperature is Manganin.

Question 27. How does specific resistance of a semi-conductor change with the increase in temperature?
Solution:
A semiconductor’s specific resistance lowers as temperature rises.

Question 28. How does (a) resistance, and (b) specific resistance of a wire depend on its (i) length, and (ii) radius?
Solution:
Resistance is inversely proportional to the square of the radius and directly proportional to the length. The specific resistance is unaffected by the wire’s size.

Question 29. Name the material used for making the connection wires. Give a reason for your answer. Why should a connection wire be thick?
Solution:
Because the resistivity of copper and aluminium is so low and the resistance of the resulting connection wires is so low, these materials are employed to make connection wires.
In order for the connecting cables’ resistance to be regarded as minimal, they are made thick.
R=ρ (I/A)
Therefore, the resistance will be lower the larger the cross-section.

Question 30. Name a material which is used for making the standard resistor. Give a reason for your answer.
Solution:
Because managing has a relatively high resistivity and the impact of temperature variation on its resistance is minimal, it is utilized to create standard resistors.

Question 31. Name the material used for making a fuse wire. Give a reason.
Solution:
Due to its high resistivity and low melting point, fuse wire is often composed of a lead and tin alloy.

Question 32. Name the material used for
(i) Filament of an electric bulb
(ii) Heating element of a room heater.
Solution:
(i) Due to its high melting point and high resistivity, tungsten wire is utilized as the filament of electric bulbs.
(ii) Because nichrome has a high resistance and a large rise in value with temperature, it is employed as a heating element for a room heater.

Question 33. What is a superconductor? Give one example of it.
Solution:
A material with zero resistance at a very low temperature is referred to be a superconductor. Mercury at 4.2 K, for instance

Question 34. A substance has zero resistance below 1 k. what is such a substance called?
Solution:
A substance has zero resistance below 1 k is called Super conductor

Exercise-8a
Multiple Choice Types

Question 1. Which of the following is an ohmic resistance?
a) LED
b) Junction diode
c) Filament of a bulb
d) Nichrome wire
Solution: d) Nichrome is an ohmic resistance.

Question 2. For which of the following substance, resistance decreases with increase in temperature?
a) Copper
b) Mercury
c) Carbon
d) Platinum
Solution: c) For carbon, resistance decreases with increase in temperature.

EXERCISE – 8A
NUMERICALS

Question 1. In a conductor 6.25 × 10¹⁶ electrons flow from its end A to B in 2s. Find the current flowing through the conductor (e = 1.6 × 10¹⁹ C)
Solution:
Number of electrons flowing through the conductor,
N = 6.25×10¹⁶ electrons
Time taken, t=2s
Given,
e = 1.6 × 10^-19 c
Let I be the current flowing through the conductor.

Question 2. A current of 1.6 mA flows through a conductor. If charge on an electron is -1.6×10^-19 coulomb, find the number of electrons that will pass each second through the cross section of that conductor
Solution:
Given that,
Current, I =1.6 mA = -1.6×10^-3A
Charge, Q = – -1.6×10^-19 Coulomb
t = 1 sec
I=Q/t
Q=I×t
Q=1.6×10^-3×1

Question 3. Find the potential difference required to pass a current of 0.2 A in a wire of resistance 20Ω
Solution:
Current (I) = 0.2 A
Resistance (R) = 20 ohm
Potential Difference (V) =?
According to Ohm’s Law:
V = IR
V = 0.2 × 20
V = 4 V

Question 4. An electric bulb draws 1.2 A current at 6.0 V. Find the resistance of filament of bulb while glowing.
Solution:
Current (I) = 1.2 A
Potential Difference/Voltage (V) = 6.0 V
Resistance (R) =?
According to Ohm’s Law:
V=IR
Then R = V/I
R=6/1.2
R = 5 Ohm

Question 5. A car bulb connected to a 12 volt battery draws 2A current when glowing. What is the resistance of the filament of the bulb? Will the resistance be more same or less when the bulb is not glowing?
Solution:
Potential Difference/Voltage (V) = 12 V
Current (I) = 2 A
Resistance (R) =?
According to Ohm’s Law:
V=IR
Then R =V/I
R = 12/2
R = 6 Ohm
Resistance will be less when the bulb is not glowing.

Question 6. Calculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
Solution:
Potential Difference/Voltage (V) = 3V
Resistance (R) = 5 ohm
Current (I) =?
According to Ohm’s Law:
V=IR
Then I=V/R
I=3/5
I=0.6A

Question 7.

Draw a characteristic V –I graph and use this graph to find:
(a) Potential difference V when the current I is 0.5 A,
(b) current I when the potential difference V is 0.75 V,
(c) resistance in circuit.
Solution:

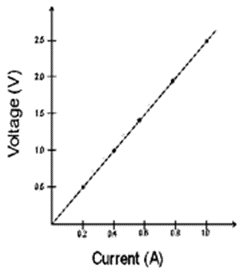
(a) 1.25 V
(b) 0.3 A
(c) The graph is linear so resistance can be found from any value of the given table. For instance:
When V = 2.5 Volt
Current is I = 1.0 amp
According to ohm’s law :
R=V/I
R=2.5/1.0
R=2.5 ohm.

Question 8. Two wires of the same material and same length have radii r1 and r2 respectively compare:
(i) Their resistances
(ii) Their resistivity
Solution:
(i) For wire of Radius

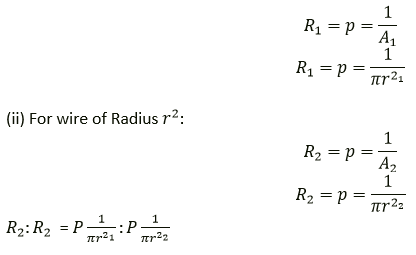
Question 9. A given wire of resistance 1Ω is stretched to double its length. What will be its new resistance?
Solution:
Let ‘I’ be the length and ‘a’ be the area of cross – section
of the resistor with resistance, R = 1Ω
When the wire is stretched to double its length,
the new length I’ = 2I and the new area of cross section,

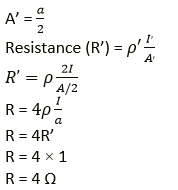
Question 10. A wire 3 ohm resistance and 10 cm length is stretched to 30 cm length. Assuming that it has a uniform cross section, what will be its new resistance?
Solution:
Resistance (R) = 3 ohm
Length l = 10 cm
New Length (l’) = 30 cm = 3 × l
R=ρ 1/A
New Resistance:
With stretching length will increase and area of cross-section will decrease in the same order

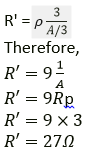
Question 11. A wire of 9 ohm resistance having 30 cm length is tripled on itself. What is its new resistance?
Solution:
It is given that,
Resistance (R) = 9 ohm
Length l = 30 cm
New Length (l) = 30 cm = 30/3 = 10 cm
R=ρ 1/A
New Resistance:
With change in length, there will be change in area of cross-section also in the same order.

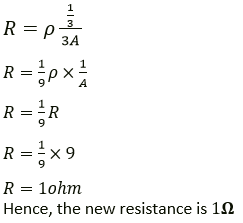
Question 12. What length of copper wire of resistivity 1.7 × 10^-8 𝛀 m and radius 1 mm is required so that its resistance is 1𝛀?
Solution:
Resistance (R) = 1 ohm
Resistivity (ρ) = 1.7 × 10-8 ohm metre
Radius (r) = 1 mm = 10-3 m
Length (l) =?

Question 13. The filament of a bulb takes a current 100 mA when potential difference across it is 0.2V. When the potential difference across it becomes 1.0 V, the current becomes 400 mA. Calculate the resistance of filament in each case and account for the difference.
Solution:
We know that,
Ohm’s law,
V=IR

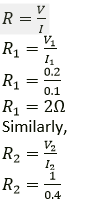
R₂ = 2.5Ω
Temperature rises cause the wire’s resistance to rise.
Hence, the difference is caused by an increase in filament temperature.

Exercise-8b

Question 1. Explain the meaning of the terms e.m.f.., terminal voltage, and internal resistance of a cell.
Solution:
E.m.f.: The potential difference between a cell’s terminals when no current is pulled from it is referred to as its electro-motive force (e.m.f).
Terminal voltage: he potential difference between a cell’s electrodes when current is extracted from it is referred to as the terminal voltage.
Internal Resistance: The internal resistance of the cell is the resistance provided by the electrolyte within to the flow of electric current through it.

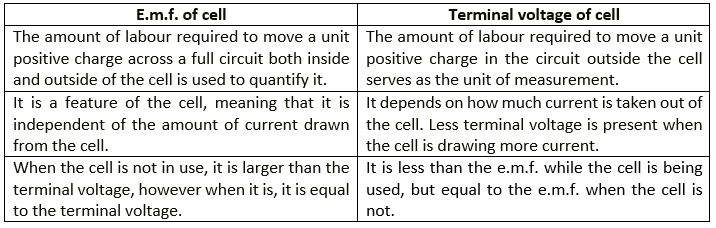
Question 2. State two differences between the e.m.f and terminal voltage of a cell
Solution:

Question 3. Name two factors on which the internal resistance of a cell depends and state how does it depend on the factors stated by you. State the factors on which the internal resistance of a cell depends.
Solution:
A cell’s internal resistance is influenced by the following variables
(i) The electrode surface area: The internal resistance decreases as the electrode surface area increases.
(ii) The distance between the electrodes: The internal resistance of the cell increases along with the electrode distance. The kind, concentration, and temperature of the solution all have an impact (electrolyte).

Question 4. A cell of e.m.f ε and internal resistance r is used to send current to an external resistance R. Write expressions for
(a) The total resistance of circuit,
(b) The current drawn from the cell.
(c) The p.d across the cell.
(d) Voltage drop inside the cell.
Solution:
(a) Total resistance = R + r
(b) Current drawn from the circuit:
We know that, ε = V+v
ε=I R+Ir
ε=I (R+r)

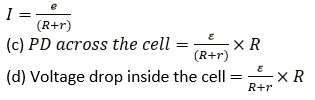
Question 5. A cell is used to send current to an external circuit.
(a) How does the voltage across its terminals compare with its e.m.f?
(b) Under what condition is the e.m.f of a cell equal to its terminal
voltage? What is e.m.f. of a cell? A cell is sending current in an external circuit. How does the terminal voltage compare with the e.m.f. of the cell?
Solution:
(a) Terminal voltage is smaller than the emf: Terminal Voltage e.m.f.
(b) When no current is drawn, the e.m.f. is equal to the terminal voltage.

Question 6. Explain why the p.d across the terminals of a cell is more in an open circuit and reduced in a closed circuit.
Solution:
Current passes across the circuit when the electric cell is in a closed circuit. Over the cell’s internal resistance, there is a potential drop. Therefore, the potential difference (p.d.) across the terminals in a closed circuit is smaller than the potential difference (p.d.) between the terminals in an open circuit by a quantity equal to the potential difference across the cell’s internal resistance.

Question 7. Write the expressions for the equivalent resistance R of three resistors R1, R2 and R3 joined in (a) parallel (b) series
Solution:
(a) Total Resistance in series: R = R₁+R₂+R₃

Question 8. How would you connect two resistors in series? Draw a diagram. Calculate the total equivalent resistance.
Solution:

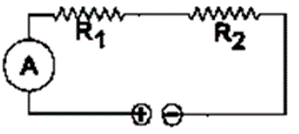
If current I is drawn from the battery, the current through each resistor will also be I.
By Applying Ohm’s law on the two resistors separately,
We have
V₁=IR₁
V₂=IR₂
V=V₁ +V₂
IR=IR₁ +IR₂
R=R₁+R₂
Total Resistance in series R
R=R₁+R₂+R₃

Question 9. Show by a diagram how two resistors R1 and R2 are joined in parallel. Obtain an expression for the total resistance of combination.
Solution:

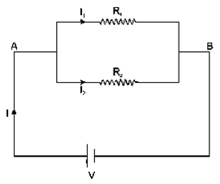
By Applying Ohm’s law on the two resistors separately,
We have,

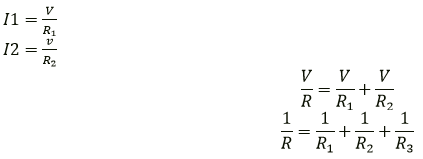
Question 10. State how are the two resistors joined with a battery in each of the following cases when:
(i) Same current flows in each resistor
(ii) Potential difference is same across each resistor
(iii) Equivalent resistance is less than either of the two resistances
(iv) Equivalent resistance is more than either of the two resistances.
Solution:
(i) Series
(ii) Parallel
(iii) Parallel
(iv) Series

Question 11. The V-I graph for a series combination and for a parallel combination of two resistors is shown in Fig – 8.38. Which of the two, A or B, represents the parallel combination? Give a reason for your answer.
Solution:
Straight line A symbolizes little resistance, but straight line B represents greater resistance, since for the same change in I, change in V for A is less than change in V for B (i.e., A is less steep than B). Resistance increases in series combination whereas it lowers in parallel combination. Therefore, A stands for the parallel combination

Exercise-8b
Multiple Choice Types

Question 1. In series combination of resistances:
a) P.d. is same across each resistance
b) Total resistance is reduced
c) Current is same in each resistance
d) All of the above are true
Solution: c) In series combination of resistances, current is same in each resistance.

Question 2. Which of the following combinations have the same equivalent resistance between X and Y?

Solution: (a) and (d)

Question 3. In parallel combination of resistances:
a) P.D. is same across each resistance
b) Total resistance is increased
c) Current is same in each resistance
d) All of the above are true
Solution: a) In parallel combination of resistances, P.D. is same across each resistance.

Exercise-8b
Numerical

Question 1. The diagram below in Fig. 8.40 shows a cell of e.m.f. ε=2 volt and internal resistance r=1 ohm to an external resistance R = 4 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when (i) the key K is open, (ii) the key K is closed.

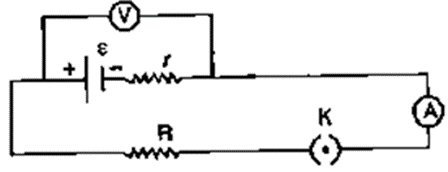
Solution:
(i) Ammeter reading = 0 because of no current
Voltage V=ϵ-Ir
V=2-0×1
V=2 volt

Question 2. A battery of e.m.f 3.0 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 1.5 A, the voltmeter reads 2.7 V. Find the internal resistance of the battery.
Solution:
It is given that,
ε = 3 volt I = 1.5 A V = 2.7 V V = ε – Ir
r=(e-V)/I
r=0.2ohm

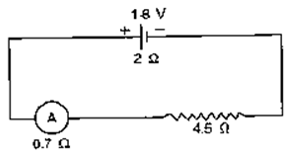
Question 3. A cell of e.m.f. 1.8V and internal resistance 2Ω is connected in series with an ammeter of resistance 0.7Ω and a resistor of 4.5Ω as shown in Fig. 8.41

Solution:
(a) ε = 1.8 V
Total Resistance = 2 + 4.5 + 0.7 = 7.2 W
I = ?

I = 0.25 A
(b) Current (calculated in (a) part) I = 0.25A
Now, total resistance excluding internal resistance = 4.5 + 0.7 = 5.2 ohm
V=IR
V=0.25×5.2
V=1.3 V

Question 4. A battery of e.m.f. 15V and internal resistance 3 ohm is connected to two resistors of resistances 3 ohm and 6 ohm is series Find:
(a) the current through the battery
(b) the p.d. between the terminals of the battery.
Solution:
(a) ε = 15 V
R = 6 + 3 = 9 ohm
r = 3 ohm
I = ?

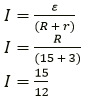
I=1.25 A
(b) Current (calculated in (a) part) I = 1.25 A
Here, External Resistance
R=R₁+R₂
R=6+3
R=9 ohm
V = IR
V = 1.25 × 9
V = 11.25 V

Question 5. A cell of e.m.f. ε and internal resistance 𝔯 sends current 1.0 A when it is connected to an external resistance 1.9Ω. But it sends current 0.5 A when it is connected to an external resistance 3.9 Ω. Calculate the values of ε and 𝔯.
Solution:
In first case it is given that,
I = 1 A,
R = 1.9 ohm
ε = I(R + r)
= 1(1.9+r)
ε = 1.9 + r___________ (1)
In second case it is given that,
I = 0.5 A,
R = 3.9 ohm
ε = I(R + r) = 0.5 (3.9 + r)
ε = 1.95 + 0.5r___________(2)
From eq. (1) and (2),
1.9 + r = 1.95 + 0.5r
r = 0.05/0.5 = 0.1 ohm
Substituting value of r
ε=1.9+r
ε=1.9+0.1
ε=2V

Question 6. Two resistors having resistance 4𝛀 and 6𝛀 are connected in parallel. Find their equivalent resistance.
Solution:
Let R be their equivalent resistance of the 4Ω and 6Ω resistors connected in parallel Then,

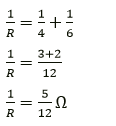
Question 7. Four resistors each of resistance 2Ω are connected in parallel. What is the effective resistance?
Solution:
R₁ = 2 ohm
R₂ = 2 ohm
R₃ = 2 ohm
R₄ = 2 ohm

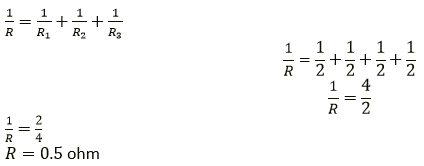
Question 8. You have three resistors of values 2Ω, 3Ω and 5Ω. How will you join them so that the total resistance is less than 1Ω? Draw diagram and find the total resistance.
Solution:
The three resistors should be connected in parallel
To get a total resistance less than 1Ω

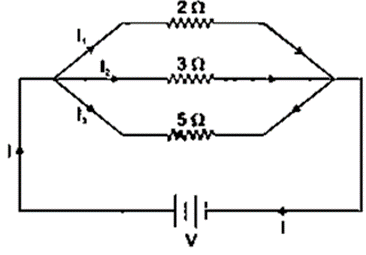
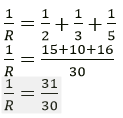
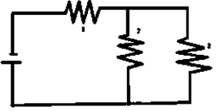
Question 9. Three resistors each of 2Ω are connected together so that their total resistance is 3Ω. Draw a diagram to show this arrangement and check it by calculation.
Solution:
A parallel combination of two resistors, in series with one resistor
R₁ = 2 ohm
R₂ = 2 ohm
R₃ = 2 ohm

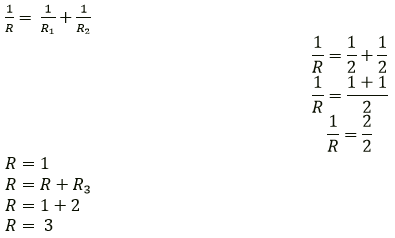
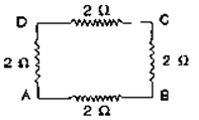
Question 10. Calculate the equivalent resistance of the following combination of resistors r₁ ,r₂ ,r₃ ,r₄ and r4 if r₁ = r₂ = r₃ = r₄= 2.0Ω between the points A and B in Fig. 8.42.

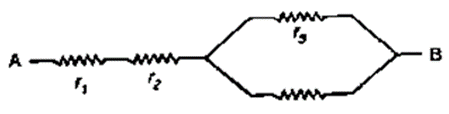
Solution:

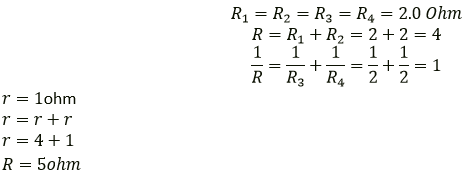
Question 11. A combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 ohm, find the resistance of the combination.
Solution:
1r = 2 + 2 + 2 = 6 ohm
2r = 2 + 2 + 2 = 6 ohm
3r = 2 + 2 + 2 = 6 ohm
4r = 2 + 2 + 2 = 6 ohm
Now these resistances are arranged in parallel:

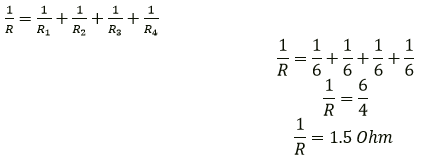
Question 12. In the circuit shown below in Fid 8.43, calculate the value of x if the equivalent resistance between A and B is 4Ω.

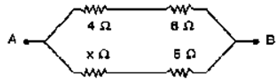
Solution:
r₁ = 4ohm
r₂ = 8ohm
r₃ = xohm
r₄ = 5ohm
r = 4ohm
r = r₁+r₂
r = 4+8
r =1₂ohm
r’= r₃+r₄
r’= (x+5) ohm

Question 13. Calculate the effective resistance between the points A and B in the circuit shown in Figure 8.44.  

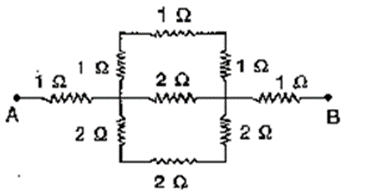
Solution:
It is given that,
Resistance between XAY = (1 + 1 + 1) = 3Ω
Resistance between XY = 2Ω
Resistance between XBY = 6Ω
Let ‘ R be the net resistance between points X and Y

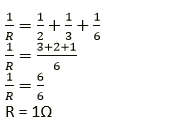
Hence, we can say that between points A and B, Three 1 Ω resistors are connected in series.
Let RAB be the net resistance between points A and B.
Then, RAB = (1 + 1 + 1)Ω
RAB = 3Ω

Question 14. A wire of uniform thickness with a resistance of 27Ω is cut into three equal pieces and they are joined in parallel. Find the equivalent resistance of the parallel combination.
Solution:
Wire cut into three pieces means new resistance =27/3
=9ohm
Now, three resistances connected in parallel:

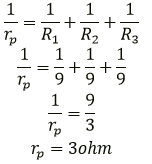
Question 15. A circuit consists of a 1 ohm resistor in series with a parallel arrangement of 6 ohm and 3 ohm resistors. Calculate the total resistance if the circuit. Draw a diagram.
Solution:

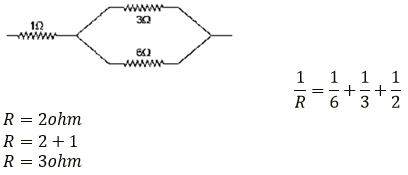
Question 16.  Calculate the effective resistance between the points A and B in the network shown below in figure.

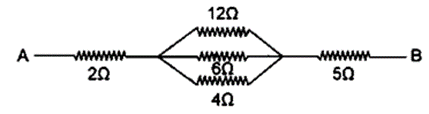
Solution:

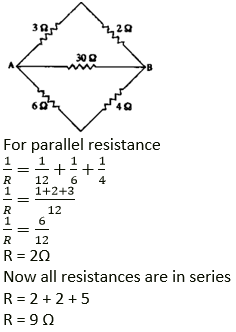
Question 17. Calculate the equivalent resistance between A and B in the adjacent diagram.
Solution:
R₁ = 3 + 2 = 5 ohm
R₂ = 30 W
R₃ = 6 + 4 = 10 ohm
R₁, R₂ and R₃ are connected in parallel

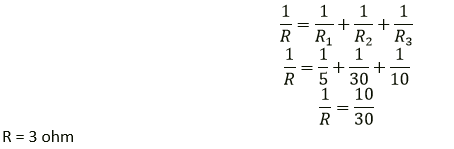
Question 18. In the network shown in following adjacent Figure, calculate the equivalent resistance between the points.
(a) A and B (b) A and C

Solution:

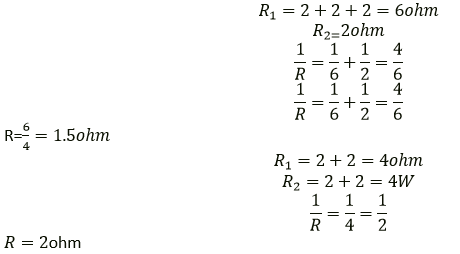
Question 19. Five resistors, each 3 Ω, are connected as shown in Fig 8.48. Calculate the resistance (a) between the points P and Q. (b) between the points X and Y.  

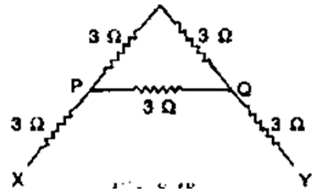
(a) R₁ = 3 + 3 = 6W
R₂ = 3W
R₁ and R₂ are connected in parallel

R=2
(b) As calculated above R=2 ohm
R₃ = 3 ohm
R₄ = 3 ohm
R’= R + R₃ + R₄
R’= 2 + 3 + 3
R’= 8 ohm

Question 20. Two resistors of 2.0Ω and 3.0Ω are connected (a) in series (b) in parallel, with a battery of 6.0 V and negligible internal resistance. For each case draw a circuit diagram and calculate the current through the battery.
Solution:
(a)

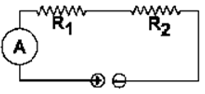
R₁= 2ohm
R₂= 3ohm
R = R₁ + R₂
R = 2 + 3
R = 5 ohm
It is given that,
V=6 V
I=V/R
I=6/5
I=1.2ohm
(b)

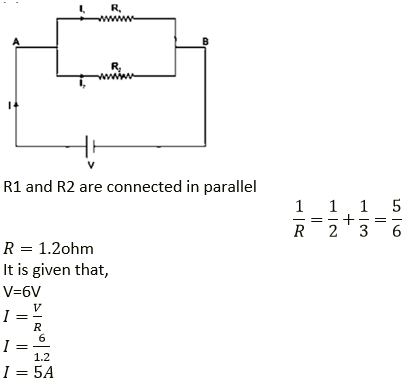
Question 21. A resistor of 6Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate (a) the current in the circuit and (b) the potential difference across the 6Ω resistor.
Solution:
(a) R₁ = 6ohm
R₂ = 4 ohm
R = R₁ + R₂
R = 6 + 4
R = 10 ohm
It is given that,
V = 20 V
I = V/R
I = 20/10
I = 2A
(b) R = 6 W
I = 2A
V =?
V = IR
V = 6 × 2
V = 12 V

Question 22. Two resistors of resistance 4 Ω and 6 Ω are connected in parallel to a cell to draw 0.5 A current from the cell.
(i) Draw a labeled diagram of the arrangement
(ii) Calculate current in each resistor.
Solution:
(i)

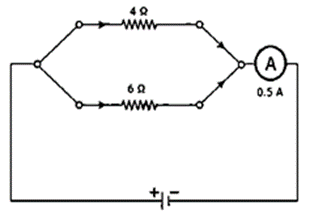
Question 23. Calculate current flowing through each of the resistors A and B in the circuit shown in following figure?

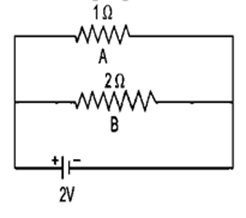
Solution:
For resistor A:
R = 1 ohm
V = 2 V
I = V/R
I = 2/1
I = 2A
For resistor B:
R = 2 ohm
V = 2 V
I = V/R
I = 2/2
I = 1A

Question 24. In figure 8.50, calculate:
(a) the total resistance of the circuit
(b) the value if R, and
(c) the current flowing in R.

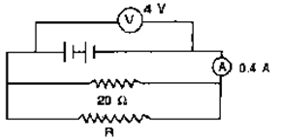
Solution:
(a) It is given that,
V = 4 V
I = 0.4 A
Total Resistance R’=?
R’ = V/I
R’ = 0.4/4
R’ = 10ohm
(b) It is given that,
R₁ = 20 ohm
R’ = 10 ohm

Question 25. A particular resistance wire has a resistance of 3 ohm per meter. Find:
(i) The total resistance of three lengths of this wire each 1.5 m long, joined in parallel.
(ii) The potential difference of the battery which gives a current of 2 A in each of the 1.5 m length when connected in the parallel to the battery (assume that resistance of the battery is negligible).
(iii) The total resistance of three lengths of this wire each 1.5 m long, in parallel.
Solution:
(i) Resistance of 1 m of wire =3 ohm
Resistance of 1.5 m of wire =3×1.5 = 4.5w

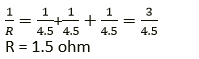
(ii) I = 2 A
V = IR = 2 x 4.5 = 9 V

(iii) R = 3 ohm for 1 m
For 5 m : R = 3 x 5 = 15 ohm
But Area A is double i.e. 2A and Resistance is inversely proportional to area so Resistance will be half.
R = 15/2 = 7.5 ohm

Question 26. A cell supplies a current of 1.2 A through two 2 Ω resistors connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate: (i) the internal resistance and (ii) e.m.f. of the cell.
Solution:
It is given that the register in the parallel
R = 1/2+1/2
R = 1 ohm
I = 1.2A
ε = I(R+r)
ε = 1.2(1+r)
ε = 1.2+1.2r……………(1)
Also, In series
R = 2+2
R = 4ohm
I = 0.4A
ε = I(R+r)
ε = 0.4(4+r)
ε = 1.6+0.4r……………(2)
By comparing equation 1 and 2
1.2 + 1.2r = 1.6 + 0.4r
1.2r-0.4r = 1.6+1.2
0.8r = 0.4
r = 0.4/0.8
r = 0.5ohm
(i) Internal resistance r = 0.5ohm
(ii) ε = I(R+r)
ε = 1.2(1+0.5)
ε = 1.8V

Question 27. A battery of e.m.f 15 V and internal resistance 3 Ω is connected to two resistors 3Ω and 6Ω connected in parallel. Find: (a) the current through the battery. (b) p.d. between the terminals of the battery, (c) the current in 3 Ω resistors, (d) the current in 6 Ω resistor.
Solution:
(a) It given that the resistors are in parallel

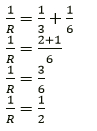
R = 2 ohm
r = 3 W ε = 15 V ε = I(R + r) 15 = I(2 + 3) I = 15/5
I = 3 A
(b) V = ?
R = 2ohm
V = IR
V = 3×2
V = 6 V
(c) V = 6V
R = 3ohm
I = V/R
I = 6/3
I = 2 A
(d) R = 6 ohm
V = 6 V I = V/R
I = 6/6
I = 1 A

Question 28. The following circuit diagram (Fig . 8.51) shows three resistors 2Ω, 4Ω and RΩ connected to a battery of e.m.f 2 V and internal resistance 3Ω. A main current of 0.25A flows through the circuit.

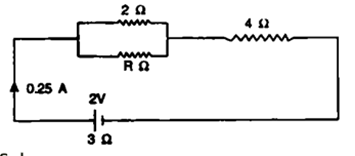
Solution:
(a) It is given that,
R = 4Ω
I = 0.25A V = IR
V = 0.25×4
V = 1V
(b) It is given that,
Internal Resistance r = 3 ohm
I = 0.25 A
V = IR
V = 0.25×3
V = 0.75 V
(c)
Effective resistance of parallel combination of two 2 ohm resistances = 1 ohm
V = I/R
V = 0.25/1
V = 0.25 V
(d) It is given that,
I = 0.25 A
ε = 2V,
r = 3 ohm
Put the values in the formula,
ε = I(R’ + r)
2 = 0.25(R’ + 3)
R’ = 5 W

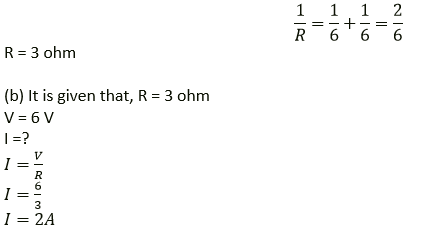
Question 29. Three resistors of 6.0 ohm, 2.0 ohm and 4.0 ohm are joined to ammeter A and a cell of emf 6.0 V as shown in following figure. Calculate:
(a) The effective resistance of the circuit.
(b) The reading of ammeter

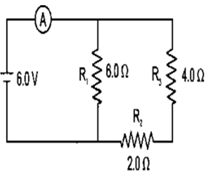
Solution:
(a)
R₁ = 6 W
R’ = R₂ + R₃ = 2 + 4 = 6 W
R₁ and R’ in parallel:

Question 30. The following diagram shows the arrangement of five different resistances connected to a battery of e.m.f. 1.8V Calculate:
(a) the total resistance of the circuit, and
(b) the reading of ammeter A.

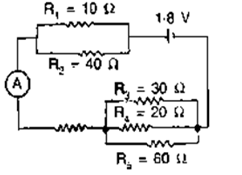
Solution:
(a) In the figure above,
Resistance between X and Y be Rxy

Question 31. A cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in following figure.

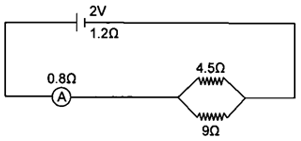
Find:
1. The reading of the ammeter,
2. The potential difference across the terminals of the cells, and
3. The potential difference across the 4.5 Ω resistor.
Solution:
The total resistance of the circuit is

Exercise-8c

Question 1. Write an expression for the electrical energy spent in flow of current through an electrical appliance in terms of current, resistance and time.
Solution:
W = I² R t joule, Electrical energy,

Question 2. Write an expression for the electrical power spent in flow of current through a conductor in terms of
(i) Resistance and potential difference.
(ii) Current and resistance.
Solution:
(i) Electrical Power, P = V²/R
(ii) Electrical Power, P = I² R

Question 3. Electrical power P is given by the expression P = (Q×V) ÷ time
(a) What do the symbols Q and V represent?
(b) Express the power P in terms of current and resistance explaining the meanings of symbols used there in.
Solution:
(a) Q stands for Charge and V for Voltage.
(b) Electricity: P = I2R, where I is current and R is resistance.

Question 4. Name the S.I. unit of electrical energy. How is it related to Why?
Solution:
The joule is the S.I. unit for electrical energy.
1Wh = 3600 J

Question 5. Explain the meaning of the statement ‘the power of an appliance is 100 W’.
Solution:
An appliance has 100 W of power. It indicates that the gadget uses 100 J of electrical energy in just one second.

Question 6. State the S.I. units of electrical power.
Solution:
Watt is the electrical power SI unit.

Question 7. (i) State and define the household unit of electricity.
(ii) What is the voltage of the electricity that is generally supplied to a house?
(iii) What is consumed while using different electrical appliances, for which electricity bills are paid?
Solution:
(i) Kilowatt-hours are the standard unit of electricity for homes (kWh). One kilowatt-hour (kWh) is the amount of electricity used by a device with a 1 kW power rating during an hour of usage.
(ii) A residence typically receives power at a voltage of 220 volts.
(iii) Electrical energy measured in kWh, also known as an electrical energy unit. Electricity is measured in units of kWh, kW, and hours.

Question 8. Name the physical quantity which is measured in (i) kW, (ii) kWh.
Solution:
KW and kWh are the units used to measure electrical power and energy, respectively.

Question 9. Define the term kilowatt – hour and state its value in S.I. unit.
Solution:
One kilowatt-hour (kWh) is the amount of electricity used by a device with a 1 kW power rating during an hour of usage.
The SI equivalent is 1 kWh = 3.6 106 J.

Q10. How do kilowatt and kilowatt-hour differ?
Solution:
Electrical energy is measured in kilowatt-hours as opposed to kilowatts, the unit of electrical power.

Question 11. Complete the following:
(i) 1 kWh = 1ampere×1volt/1000
(ii) 1 kWh = _________ J
Solution:
(i) 1hour
(ii) 3.6 x 10⁶

Question 12. What do you mean by power rating of an electrical appliance? How do you use it to calculate?
(a) The resistance of the appliance and
(b) An electrical appliance such as electric bulb, geyser etc. is rated with power (P) and voltage (V) which is known as its power rating. For example: If an electric bulb is rated as 50W-220V, it means that when the bulb is lighted on a 220 V supply, it consumes 50 W electrical power.
Solution:
(a) The following expression should be used to determine the appliance’s resistance:
Resistance, R =V²/P
(b) The safe limit of current I is : I =P/V

Question 13. An electric bulb is marked ‘100 W, 250 V’. What information does this convey?
Solution:
It signifies that 100 W of electricity is used to illuminate the bulb when it is powered by a 250 V source (which means 100J of electrical energy is converted in the filament of bulb into the light and heat energy in 1 second).

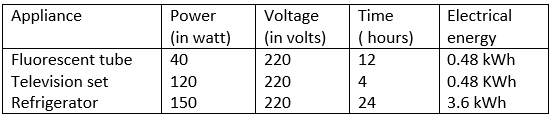
Question 14. List the names of three electrical gadgets used in your house. Write their power, voltage rating and approximate time for which each one is used in a day. Hence find the electrical energy consumed by each in day.
Solution:

Question 15. Two lamps, one rated 220 V, 50 W and the other rated 220 V, 100 W, are connected in series with mains of 220 V. Explain why does the 50 W lamp consume more power.
Solution:
Resistance of 220 V, 50 W lamps is

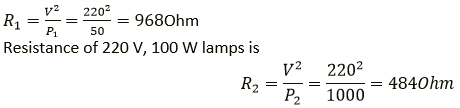
Since the two lamps are connected in series
so same current I passes through each lamp.
Power consumed in 220 V, 50 W lamp is P₁ = I²R₁
Power consumed in 220 V, 100 W lamp is P₂ = I²R₂
Since R¹>R², P¹>P²
i.e. 50 W lamps consume more power.

Question 16. Name the factors on which the heat produced in a wire depends when current is passed in it, and state how it depends on the factors stated by you.
Solution:
Three elements determine how much heat is generated in a wire when current flows through it:
Based on three factors: the wire’s resistance, the amount of current flowing through it, and the duration of that current flow
(i) Heat created in a wire is dependent on the current flowing through it; specifically, the quantity of heat H produced in a wire is exactly proportional to the square of the current I flowing through it, i.e., H α I²
(ii) Heat production is dependent on wire resistance; specifically, the relationship between heat production (H) and wire resistance (R) is i.e., H α R
(iii) The quantity of heat H created in the wire is exactly proportional to the duration of time t during which current is conducted through the wire, i.e., H∝t

Exercise-8c
Multiple Choice Types

Question 1. When a current I flows through a resistance R for time t, the electrical energy spent is given by:
a) IRt
b) I²Rt
c) IR²t
d) I²R/t
Solution: b) I²Rt
Note: Electrical energy (W) = I²Rt = VIt = V² t/R

Question 2. An electrical appliance has a rating 100 W, 120V. The resistance of element of appliance when in use:
a) 1.2 Ω
b) 144 Ω
c) 120 Ω
d) 100 Ω
Solution:
144 Ω
Given, Power (P) = 100 W
Potential difference, V = 120 volt

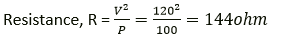
Exercise-8c
Numerical

Question 1. An electric bulb of resistance 500 Ω draws current 0.4 A from the source. Calculate:
(a) the power of bulb and
(b) the potential difference at its end.
Solution:
Resistance of electric bulb (R) = 500Ω
Current drawn from the source (I) = 0.4 A
Power of the bulb (P) = VI
V = I x R
V = 0.4 x 500 = 200 V
The potential difference at its end is 200 V.
Hence,
Power (P) = VI
P = 200 x 0.4 = 80 W
The power of the bulb is 80 Watt.

Question 2. A current of 2 A is passed through a coil of resistance 75 Ω for 2 minutes.
(a) How much heat energy is produced?
(b) How much charge is passed through the resistance?
Solution:
It is given, current (I) = 2 A
Resistance R = 75 Ω
Time, t = 2 min = 120 s
(a) Heat produced, H = I²Rt
H = (2)² (75)(120) J
H = 36000 J
(b) Charge passed, Q = It
Q = (2)(120)
C = 240 C

Question 3. Calculate the current through a 60 W lamp rated 250 V. If the line voltage falls to 200 V, how is power consumed by the bulb affected?
Solution:
It is given that,
Power P = 60 W
Voltage, V = 250 V
As Power, P = VI

Question 4. An electric bulb is rated ‘100 W, 250 V’. How much current will the bulb draw if connected to a 250 V supply?
Solution:
It is given that,
Power P = 100 W
Voltage V = 250 V
As Power, P = VI
I = 100/250
I = 0.4A

Question 5. An electric bulb is rated at 220 V, 100 W.
(a) What is its resistance?
(b) What safe current can be passed through it?
Solution:
(a) It is given that,
Power P = 100 W
Voltage V = 220 V
As power, P = V^2/R
R = 220²/100
R = 484
(b) The safe limit of current that can pass through it
I = P/V
I = 100/220 = 0.45A

Question 6. A bulb of 40 W is used for 12.5 h each day for 30 days. Calculate the electrical energy consumed.
Solution:
Energy consumed per day, E = P × t
= 40 × 12.5
= 500 Wh
Energy consumed for 30 days
E = 500 × 30
E = 15000 Wh
E = 15 kWh.

Q7. An electric iron is rated 750 W, 230 V. Calculate the electrical energy consumed by the iron in 16 hours.
Solution:
Here energy will be,
E = Power × time
E = 750 × 16
E = 12000 Wh
E = 12 kWh

Question 8. An electrical appliance having a resistance of 200 Ω is operated at 220 V. Calculate the energy consumed by the appliance in 5 minutes.
(i) In joules. (ii) In kWh.
Solution:
(i) Given, Resistance, R = 200 Ω
Voltage, V = 200 V
Time, t = 5 min = 5 × 60 sec = 300 sec

Question 9. A bulb marked 12 V, 24 W operates on a 12 V battery for 20 minutes. Calculate:
(i) The current flowing through it, and
(ii) The energy consumed.
Solution:
(a) Given,
Power, P = 24 W
Voltage, V = 12 V
Current, I = ?
As power, P = VI

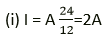
(ii) Energy, E = P × t
E = 24 × 20 × 60 sec
E = 28800 J

Question 10. A current of 0.2 A flows through a wire whose ends are at a potential difference of 15 V. Calculate:
(i) The resistance of the wire, and
(ii) The heat energy produced in 1 minute.
Solution:
Given,
Current, I = 0.2 A
Potential difference, V = 15 V
Time, t = 60 sec
As V = IR
(a) R=150/72
R = 75 Ω
(b) Heat energy, H = I²Rt
H = (0.2)² × 75 × 60
H = 180 J

Question 11. What is the resistance, under normal working conditions, of an electric lamp rated at ‘240 v, 60 W’? If two such lamps are connected in series across a 240 V mains supply, explain why each one appears less bright.
Solution:
It is given that, Voltage, V = 240 V
Power, P = 60 W

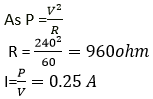
When one lamp is connected across the mains, it draws 0.25 A current, while if two lamps are connected in series across the mains, current through each bulb becomes

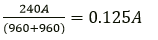
(i.e., current is halved), hence heating (= I²Rt) in each bulb becomes one-fourth, so each bulb appears less bright.

Question 12. Two bulbs are rated 60 W, 220 V and 60 W, 110 V respectively. Calculate the ratio of their resistances.
Solution:
It is given that,
Voltage, V₁ = 220 V
V₂ = 110 V
Power, P₁ = P₂ = P = 60 W

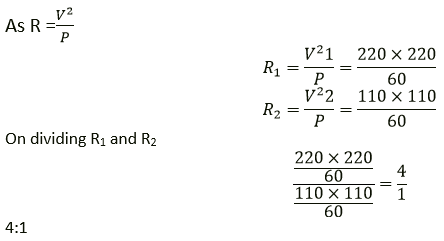
Question 13. An electric bulb is rated 250 W, 230 V.
(i) The energy consumed in one hour, and
(ii) The time in which the bulb will consume 1.0 kWh energy when connected to 230 V mains.
Solution:
Given,
Power, P = 250 W
Voltage, V = 230 V
(i) Energy, E = P × t
Time, t = 1000/250 = 4 hours
If it comes 1 kWh of energy then it requires 4 hours.

Question 14. Three heaters each rated 250 W, 100 V are connected in parallel to a 100 V supply. Calculate:
(i) The total current taken from the supply
(ii) The resistance of each heater
(iii) The energy supplied in kWh to the three heaters in 5 hours.
Solution:
(i) It is given that,
Power, P = 250 W
Voltage, V = 100 V
Current through each heater, I = ?
As P = VI
The total current taken from the supply
I = P/V
I = 250/100
I = 2.5 A
Current taken for the three heaters = 3×2.5 = 7.5 A
(ii) Given,
Power, P = 250 W
Voltage, V = 100 V
Resistance for each heater R = V/I
100/2.5 = 40Ohm
(iii) Given,
Power, P = 250 W
Voltage, V = 100 V
Time for which energy is supplied, t = 5 h
As, Energy E = P × t
E = 250 × 5 = 1250 Wh
Or E = 1.25 kWh
Energy for three heaters = 3 × 1.25 = 3.75 kWh

Question 15. A bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate:
(i) The total energy supplied by the battery in 10 minutes
(ii) The resistance of the bulb
(iii) The energy dissipated in the bulb in 10 minutes.
Solution:
(i) Given,
Voltage, V = 4 V
Resistance of the battery, RB = 2.5 Ω
Current, I = 0.5 A

(ii) Given,
Voltage, V = 4 V
Resistance of the battery, RB = 2.5 Ω
Current, I = 0.5 A
Total resistance, R = 8 Ω
Resistance of the battery, RB = 2.5 Ω
Resistance of the blub, Rb = 8 – 2.5 Ω = 5.5 Ω
(iii) Given,
Voltage, V = 4 V
Resistance of the battery, RB = 2.5 Ω
Current, I = 0.5 A
Energy dissipated in the bulb in 10 min, E = I2Rt
E = (0.5)² × 5.5 × 600 = 825 J

Question 16. Two resistors A and B of 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate:
(i) The power supplied by the battery.
(ii) the power dissipated in each resistor.
Solution:
(i) Given,
Resistance, R_A = 4 Ω
Resistance, R_B = 6 Ω
Voltage, V = 6 V
Ω AS resistances are connected in parallel

Question 17. A battery of e.m.f. 15 V and internal resistance 2 Ω is connected to two resistors of resistances 4 ohm and 6 ohm joined (a) in series. Find in each case the electrical energy spent per minute in 6 Ω resistors.
Solution:
Given, E.m.f of battery, V = 15 V
Internal resistance of battery, R_B = 2 Ω
Resistance given in circuit, R₁ = 4 Ω
R₂ = 6 Ω
(i) When resistors are connected in series,
Equivalent resistance, R = R_B + R₁ + R₂ = 12 Ω
Current in the circuit, I = 15/12 = 1.25 A
Now voltage across resistor R₂, V₂ = IR = 1.25 × 6
V₂ = 7.50 V
Time, t = 1 min = 60 sec

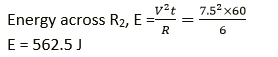
Question 18. Water in an electric kettle connected to a 220 V supply took 5 minutes to reach its boiling point. How long would it have taken if the supply had been of 200 V?
Solution:

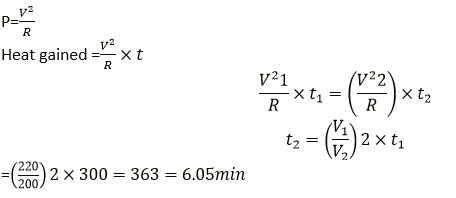
Question 19. An electric toaster draws 8 A current in a 220 V circuit. It is used for 2 hr. Find the cost of operating the toaster if the cost of electrical energy is Rs. 4.50 per kWh.
Solution:
Given:
Voltage (V) = 220 V
Current (I) = 8 A
Time (t) = 2 h
Energy (E) = Volt = 220 × 8 × 2 = 3.52 kWh
The cost per kWh is Rs. 4.50
Hence, the cost of running the kettle for two hours is: 3.52 × 4.50 = Rs. 15.84

Question 20. An electric kettle is rated 2.5 kW, 250 V. Find the cost of running the kettle for two hours at Rs. 5.40 per unit.
Solution:
Given,
Power of kettle, P = 2.5 kW
Voltage, V = 250 V
Time, t = 2 h
As, Energy , E = P × t
= 2.5 × 2 = 5 kWh
Cost per unit of energy = Rs 5.40
Cost for 5 kWh of energy = 5.40 × 5 = Rs 27

Question 21. A geyser is rated 1500 W, 250 V. This geyser is connected to 250 V mains. Calculate:
(i) The current drawn,
(ii) The energy consumed in 50 hours, and
(iii) The cost of energy consumed at Rs 4.20 per kWh.
Solution:
Given,
Power of geyser, P = 1500 W
Voltage, V = 250 V

(ii) Time, t = 50 h
Energy, E = P × t
E = 1500 × 50
E = 75000 Wh
E = 75 kWh
(iii) Cost per unit of energy = Rs 4.20
Cost for 75 kWh of energy = 4.20 × 75 = Rs 315